聚类算法

2019-01-10

1 K-Means

设计目的：使各个样本与所在簇的质心的均值的误差平方和达到最小。

\[SSE=\sum\limits_{i=1}^{k}\sum\limits_{x\in C_i}||x-\mu_i||_2^2\]

表示样本点$x$到cluster $C_i$的质心$c_i$距离平方和；最优的聚类结果应使得SSE达到最小值。

算法步骤：

  1. 从D中随机取k个元素，作为k个簇的各自的中心。
  2. 分别计算剩下的元素到k个簇中心的相异度（一般使用欧氏距离），将这些元素分别划归到相异度最低的簇。
  3. 根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。
  4. 将D中全部元素按照新的中心重新聚类。
  5. 重复第4步，直到聚类结果不再变化。
  6. 将结果输出。

kmeans

优点：

  1. 算法简单，容易实现
  2. 对处理大数据集，该算法是相对可伸缩和高效率的，因为他的复杂度大约是$O(nkt)$，其中n是所有对象的数目，k是簇的数目，t是迭代次数，通常$k<<n$。这个算法通常局部收敛。
  3. 算法尝试找出使平方误差函数最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。

缺点：

  1. 对数据类型要求较高，是和数值型数据。
  2. 可能收敛到局部最小值，在大规模数据上收敛较慢。
  3. k值比较难以选取。
  4. 对初值的簇心值敏感，对不同的初始值，可能会导致不同的聚类结果。不能保证Ｋ-Means算法收敛于全局最优解。
    • 针对此问题，在K-Means的基础上提出了二分K-means算法。该算法首先将所有点看做是一个簇，然后一分为二，找到最小SSE的聚类质心。接着选择其中一个簇继续一分为二，此处哪一个簇需要根据划分后的SSE值来判断。

参考文献：
算法杂货铺——k均值聚类(K-means)
【十大经典数据挖掘算法】k-means
机器学习算法-K-means聚类

2 高斯混合概率（GMM）

3 密度聚类（DBSCAN算法）

密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN基于一组“领域”参数($\epsilon,MinPts$)来刻画样本分布的紧密程度。给定数据集$D=\{x_1, x_2, ..., x_m\}$，定义下面几个概念：

  1. $\epsilon$-邻域：对$x_j \in D$，其中$\epsilon$-邻域包含样本集$D$中与$x_j$距离不大于$\epsilon$的样本，即$N_\epsilon(x_j)=\{x_j\in D|dist(x_i,x_j)\leq\epsilon\}$；
  2. 核心对象：若$x_j$的$\epsilon$-邻域至少包含$MinPts$个样本，即$|N_\epsilon(x_j)|\geq MinPts$，则$x_j$是一个核心对象;　
  3. 密度直达：:若$x_j$位于$x_i$的$\epsilon$-邻域中，且$x_i$是核心对象，则称$x_j$由$x_i$密度直达;
  4. 密度可达：对$x_i$与$x_j$，若存在样本序列$p_1,p_2,...,p_n$，其中$p_1=x_i$，$p_n=x_j$且$p_{i+1}$由$p_i$密度直达，则称$x_j$由$x_i$密度可达;
  5. 密度相连：对$x_i$与$x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$x_i$与$x_j$密度相连。

概念

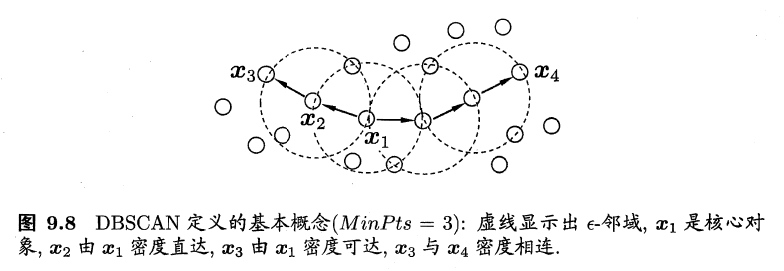
DBSCAN将”簇”定义为:由密度可达关系导出的最大的密度相连样本集合。形式化地说，给定邻域参数($\epsilon,MinPts$)，簇$C\subseteq D$是满足以下性质的非空样本子集:

  • 连接性(connectivity): $x_i\in C$，$x_j\in C\implies$ $x_i$与$x_j$密度相连；
  • 最大性(maximality): $x_i\in C$，$x_j$由$x_i$密度可达 $\implies$ $x_j\in C$。

实际上，若$x$为核心对象，由$x$密度可达的所有样本组成的集合记为$X=\{\overline x\in D\}$，其中$\overline x$和$x$密度可达，则不难证明$X$即为满足连接性与最大性的簇。

DBSCAN 算法先任选数据集中的一个核心对象为”种子”(seed)，再由此出发确定相应的聚类簇，算法描述如下。

  • 在第1至7行中，算法先根据给定的邻域参数($\epsilon,MinPts$)找出所有核心对象；
  • 在第10至24行中，以任一模心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。

DBSCAN

优点：

  1. 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。
  2. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
  3. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

缺点：

  1. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合
  2. 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
  3. 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

4 层次聚类（AGNES算法）

层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。具体又可分为：

  • 凝聚的层次聚类：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。
  • 分裂的层次聚类：采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。

AGNES 是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的，两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。这里的关键是如何计算聚类簇之间的距离。

算法步骤：

  1. （初始化）把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；
  2. 寻找各个类之间最近的两个类，把他们归为一类（这样类的总数就少了一个）；
  3. 重新计算新生成的这个类与各个旧类之间的相似度；
  4. 重复2和3直到所有样本点都归为一类，结束。

距离计算： 例如给定聚类簇$C_i$和$C_j$，两个簇的距离可以通过以下定义得到： 距离计算

算法伪代码

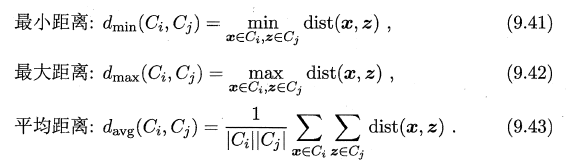
优点：

  • 一次性得到聚类树，后期再分类无需重新计算；
  • 相似度规则容易定义；
  • 可以发现类别的层次关系。

缺点：

  • 计算复杂度高，不适合数据量大的；
  • 算法很可能形成链状。

参考文献：
机器学习算法-层次聚类AGNES
聚类算法之层次聚类（Python实现）