深度优先搜索和广度优先搜索

2019-01-05

数据结构与算法

1 深度优先搜索（DFS）

深度优先搜索，从初始访问结点出发，我们知道初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点。

深度优先搜索需要使用栈结构来存储访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。总结起来可以这样说：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。

我们从这里可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。

算法步骤：

访问顶点v；
依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

1.1 无向图的深度优先搜索

下面以”无向图”为例，来对深度优先搜索进行演示。
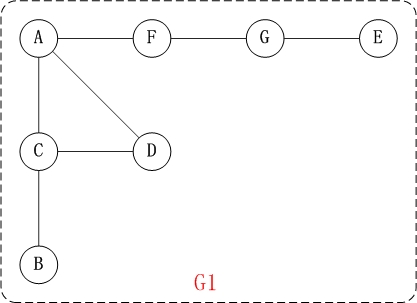
无向图结构
对上面的图G1进行深度优先遍历，从顶点A开始。

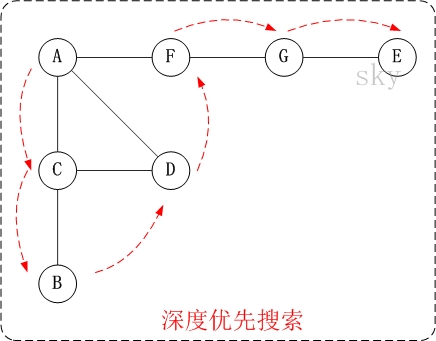
第1步： 访问A。
第2步： 访问(A的邻接点)C。
- 在第1步访问A之后，接下来应该访问的是A的邻接点，即”C,D,F”中的一个。但在本文的实现中，顶点ABCDEFG是按照顺序存储，C在”D和F”的前面，因此，先访问C。
第3步： 访问(C的邻接点)B。
- 在第2步访问C之后，接下来应该访问C的邻接点，即”B和D”中一个(A已经被访问过，就不算在内)。而由于B在D之前，先访问B。
第4步： 访问(C的邻接点)D。
- 在第3步访问了C的邻接点B之后，B没有未被访问的邻接点；因此，返回到访问C的另一个邻接点D。
第5步： 访问(A的邻接点)F。
- 前面已经访问了A，并且访问完了”A的邻接点B的所有邻接点(包括递归的邻接点在内)”；因此，此时返回到访问A的另一个邻接点F。
第6步： 访问(F的邻接点)G。
第7步： 访问(G的邻接点)E。

因此访问顺序是：A -> C -> B -> D -> F -> G -> E

1.2 有向图的深度优先搜索

下面以”有向图”为例，来对深度优先搜索进行演示。
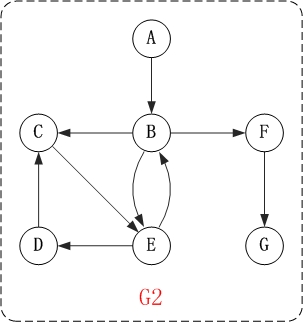
有向图结构
对上面的图G2进行深度优先遍历，从顶点A开始。

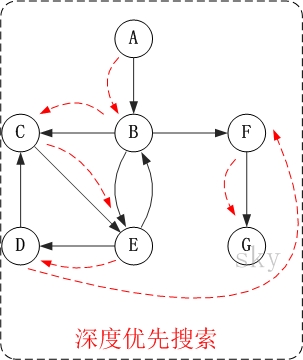
第1步： 访问A。
第2步： 访问B。
- 在访问了A之后，接下来应该访问的是A的出边的另一个顶点，即顶点B。
第3步： 访问C。
- 在访问了B之后，接下来应该访问的是B的出边的另一个顶点，即顶点C,E,F。在本文实现的图中，顶点ABCDEFG按照顺序存储，因此先访问C。
第4步： 访问E。
- 接下来访问C的出边的另一个顶点，即顶点E。
第5步： 访问D。
- 接下来访问E的出边的另一个顶点，即顶点B,D。顶点B已经被访问过，因此访问顶点D。
第6步： 访问F。
- 接下应该回溯”访问A的出边的另一个顶点F”。
第7步： 访问G。

因此访问顺序是：A -> B -> C -> E -> D -> F -> G

2 广度优先搜索（BFS）

类似于一个分层搜索的过程，广度优先搜索需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。算法步骤：

访问顶点v
依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。
如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

2.1 无向图的广度优先搜索

下面以”无向图”为例，来对广度优先搜索进行演示。还是以上面的图G1为例进行说明。

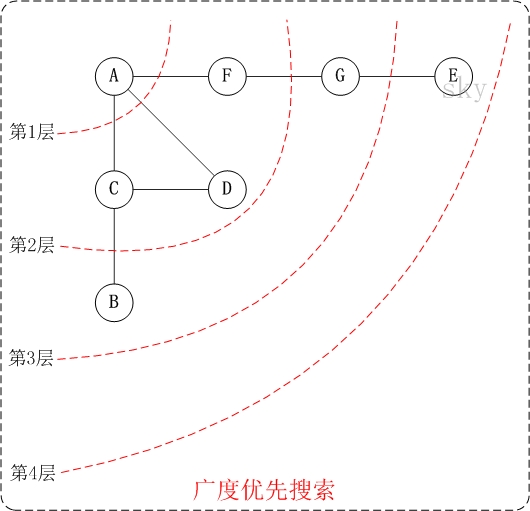
第1步： 访问A。
第2步： 依次访问C,D,F。
- 在访问了A之后，接下来访问A的邻接点。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，C在”D和F”的前面，因此，先访问C。再访问完C之后，再依次访问D,F。
第3步： 依次访问B,G。
- 在第2步访问完C,D,F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再访问F的邻接点G。
第4步： 访问E。
- 在第3步访问完B,G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻接点E。

因此访问顺序是：A -> C -> D -> F -> B -> G -> E

2.2 有向图的广度优先搜索

下面以”有向图”为例，来对广度优先搜索进行演示。还是以上面的图G2为例进行说明。

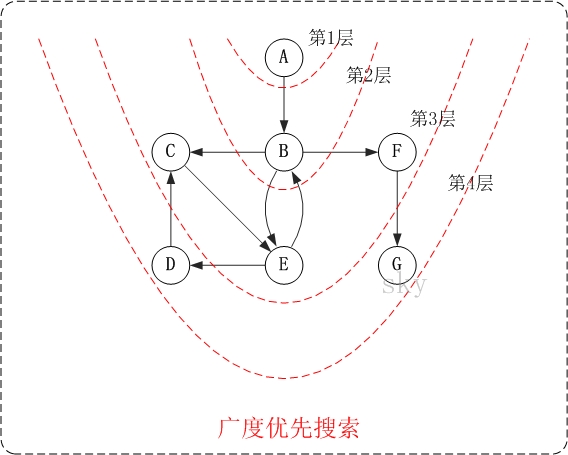
第1步： 访问A。
第2步： 访问B。
第3步： 依次访问C,E,F。
- 在访问了B之后，接下来访问B的出边的另一个顶点，即C,E,F。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，因此会先访问C，再依次访问E,F。
第4步： 依次访问D,G。
- 在访问完C,E,F之后，再依次访问它们的出边的另一个顶点。还是按照C,E,F的顺序访问，C的已经全部访问过了，那么就只剩下E,F；先访问E的邻接点D，再访问F的邻接点G。

因此访问顺序是：A -> B -> C -> E -> F -> D -> G

3 实现

# 使用广度优先搜索和深度优先搜索遍历二叉树
# -*- coding: utf-8 -*-
class BinaryTree(object):
    def __init__(self, data):
        self.__key = data
        self.__leftChild = None
        self.__rightChild = None

    def getKey(self):
        return self.__key

    def getLeft(self):
        return self.__leftChild

    def setLeft(self, tree):
        self.__leftChild = tree

    def getRight(self):
        return self.__rightChild

    def setRight(self, tree):
        self.__rightChild = tree

    def insertLeft(self, data):
        if self.__leftChild == None:
            self.setLeft(BinaryTree(data))
        else:
            t = BinaryTree(data)
            t.setLeft(self.getLeft())
            self.setLeft(t)

    def insertRight(self, data):
        if self.__rightChild == None:
            self.setRight(BinaryTree(data))
        else:
            t = BinaryTree(data)
            self.setRight(self.getRight())
            self.setRight(t)

# 深度优先搜索
def DFS(root):
    if not root:
        return []
    nodelist = []  # 存储遍历的结果
    stack = []  # 模拟栈
    stack.append(root)
    # 当栈不为空时
    while stack:
        # 取出栈顶节点
        tmp = stack.pop()
        nodelist.append(tmp.getKey())
        # 因为栈是先入后出的，左节点要比右节点先访问，所以先把右节点入栈，再把左节点入栈
        if tmp.getRight():
            stack.append(tmp.getRight())
        if tmp.getLeft():
            stack.append(tmp.getLeft())
    return nodelist

# 广度优先搜索
def BFS(root):
    if root == None:
        return []
    queue = []  # 模拟队列
    nodelist = []  # 存储遍历的结果
    node = root
    queue.append(node)
    while queue:
        node = queue.pop(0)
        nodelist.append(node.getKey())
        if node.getLeft():
            queue.append(node.getLeft())
        if node.getRight():
            queue.append(node.getRight())
    return nodelist

4 总结

一般来说，能用DFS解决的问题，都能用BFS。

DFS多用于连通性问题因为其运行思想与人脑的思维很相似，故解决连通性问题更自然。
BFS多用于解决最短路问题，其运行过程中需要储存每一层的信息，所以其运行时需要储存的信息量较大，如果人脑也可储存大量信息的话，理论上人脑也可运行BFS。

总的来说多数情况下运行BFS所需的内存会大于DFS需要的内存(DFS一次访问一条路，BFS一次访问多条路)，DFS容易爆栈(栈不易”控制”)，BFS通过控制队列可以很好解决”爆队列”风险。

参考文献

图的遍历之深度优先搜索和广度优先搜索
 图的理解：深度优先和广度优先遍历及其 Java 实现
 图的广度优先和深度优先遍历（BFS和DFS）
图的基础遍历：深度优先和广度优先

 查找算法总结 K-最邻近算法(分类) 