查找算法分类：

1. 静态查找和动态查找：静态或者动态都是针对查找表而言的。
   • 静态查找：如本篇要介绍的顺序查找、二分查找和分块查找；
   • 动态查找：动态表指查找表中有删除和插入操作的表。如本篇要介绍的树表查找(二叉树查找、平衡查找树之2-3查找树、平衡查找树之红黑树、B树和B+树查找)和哈希查找。
2. 无序查找和有序查找：
   • 无序查找：被查找数列有序无序均可；
   • 有序查找：被查找数列必须为有序数列。

平均查找长度(Average Search Length，ASL)：需和指定$key$进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。

对于含有$n$个数据元素的查找表，查找成功的平均查找长度为：$ASL=\sum\limits_{i=1}^nP_i*C_i$。

• $P_i$：查找表中第$i$个数据元素的概率。
• $C_i$：找到第$i$个数据元素时已经比较过的次数。

1 顺序查找

说明： 顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想： 顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值$k$相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于$k$的结点，表示查找失败。
复杂度分析： 查找成功时的平均查找长度为：（假设每个数据元素的概率相等）

当查找不成功时，需要$n+1$次比较，时间复杂度为$O(n)$；所以，顺序查找的时间复杂度为$O(n)$。

代码实现：

# 顺序查找
def SequenceSearch(mlist, key):
    for i in range(len(mlist)):
        if mlist[i] == key:
            return i
    return -1

优缺点：

• 缺点：是当$n$很大时，平均查找长度较大，效率低；
• 优点：是对表中数据元素的存储没有要求。另外，对于线性链表，只能进行顺序查找。

2 二分查找

说明： 元素必须是有序的，如果是无序的则要先进行排序操作。
基本思想： 也称为是折半查找，属于有序查找算法。用给定值$k$先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据$k$与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。
复杂度分析： 最坏情况下，关键词比较次数为$\log_2(n+1)$，且期望时间复杂度为$O(\log_2n)$；

折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。 ——《大话数据结构》

代码实现：

# 二分查找，非递归
def BinarySearch1(mlist, key):
    left = 0
    right = len(mlist) - 1
    while left <= right:
        mid = (left + right) // 2
        if mlist[mid] == key:
            return mid
        elif mlist[mid] > key:
            right = mid - 1
        elif mlist[mid] < key:
            left = mid + 1
    return -1

# 二分查找，递归
def BinarySearch2(mlist, key, start, end):
    if start <= end:
        mid = (start + end) // 2
        if nums[mid] == target:
            return mid
        elif nums[mid] > target:
            return BinarySearch2(nums, target, start, mid - 1)
        else:
            return BinarySearch2(nums, target, mid + 1, end)
    else:
        return -1

优缺点：

• 优点：比较次数少，查找速度快，平均性能好;
• 缺点：是要求待查表为有序表，且插入删除困难。

3 插值查找

说明： 数据必须采用顺序存储结构，数据必须有序。

二分查找每次都从中间开始搜索，这种查找方式显得不够智能，无法很好地处理当查找的数值位于最前面或最后面这种情况。二分查找中查找点计算如下：

即:

通过类比，我们可以将查找的点改进为如下：

也就是将上述的比例参数$\dfrac{1}{2}$改进为自适应的，根据关键字在整个有序表中所处的位置，让$mid$值的变化更靠近关键字$key$，这样也就间接地减少了比较次数。

基本思想： 基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，差值查找也属于有序查找。

对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

复杂度分析： 查找成功或者失败的时间复杂度均为$O(\log_2(\log_2n))$。 代码实现：

# 插值查找
def InsertionSearch(mlist, key, left, right):
    mid = left + ((key - mlist[left]) // (mlist[right] - mlist[left])) * (right - left)
    if mlist[mid] == key:
        return mid
    elif mlist[mid] > key:
        return InsertionSearch(mlist, key, left, mid - 1)
    elif mlist[mid] < key:
        return InsertionSearch(mlist, key, mid + 1, right)

4 斐波那契查找

说明： 数据必须采用顺序存储结构，数据必须有序。
基本思想： 也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数与某个斐波那契数差值为$1$，即$n=F(k)-1$，所以需要将数组扩展到$F(k)-1$的长度。

开始将$key$值与第$F(k-1)$位置的记录进行比较，即$mid=low+F(k-1)-1$，比较结果也分为三种：

1. 相等，mid位置的元素即为所求
2. 大于，则$low=mid+1,k-=2$。说明：$low=mid+1$说明待查找的元素在$[mid+1,high]$范围内，$k-=2$说明范围$[mid+1,high]$内的元素个数为$n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1$个，所以可以递归的应用斐波那契查找。
3. 小于，则$high=mid-1,k-=1$。说明：$low=mid-1$说明待查找的元素在$[low,mid-1]$范围内，$k-=1$说明范围$[low,mid-1]$内的元素个数为$F(k-1)-1$个，所以可以递归的应用斐波那契查找。

复杂度分析： 最坏情况下，时间复杂度为$O(\log_2n)$，且其期望复杂度也为$O(\log_2n)$。
代码实现：

# 斐波那契查找
def F(num):
    if num <= 2:
        return [1] * num
    else:
        Fibonacci = [1, 1]
        for i in range(2, num):
            Fibonacci.append(Fibonacci[i-1] + Fibonacci[i-2])
        return Fibonacci

def FibonacciSearch(mlist, key):
    length = len(mlist)  # 数组长度
    left = 0
    right = length - 1

    Fibonacci = F(length)  # 构造一个斐波那契数列
    # 计算数组 mlist长度值(length)位于斐波那契数列的位置
    k = 0
    while length > Fibonacci[k] - 1:
        k += 1
    # 将数组 mlist扩展到 Fibonacci[k]-1的长度
    mlist.extend(mlist[-1:] * (Fibonacci[k] - 1 - length))
    while left <= right:
        mid = left + Fibonacci[k-1] - 1
        if key < mlist[mid]:
            right = mid - 1
            k -= 1
        elif key > mlist[mid]:
            left = mid + 1
            k -= 2
        else:
            if mid < length:
                return mid  # 若相等则说明 mid即为查找到的位置
            else:
                return length - 1  # 若 mid>=length则说明是扩展的数值,返回 length-1
    return -1

5 树表查找

5.1 二叉查找树

基本思想： 二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后和每个节点的父节点比较大小，查找最适合的范围。这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

二叉查找树具有下列性质：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树。

对二叉查找树进行中序遍历，即可得到递增的数列。

复杂度分析： 它和二分查找一样，插入和查找的时间复杂度均为$O(\log_2n)$，但是在最坏的情况下仍然会有$O(n)$的时间复杂度。

代码实现：
首先是二叉查找树的节点定义。

class BinarySearchTree(object):
    def __init__(self, key):
        self.__key = key
        self.__leftChild = None
        self.__rightChild = None
        self.__parent = None  # 父节点

接下来是生成二叉查找树。

def insert(self, data):
    if data < self.getKey():
        if self.getLeftChild():
            self.getLeftChild().insert(data)
        else:
            tree = BinarySearchTree(data)
            tree.setParent(self)
            self.setLeftChild(tree)
    elif data > self.getKey():
        if self.getRightChild():
            self.getRightChild().insert(data)
        else:
            tree = BinarySearchTree(data)
            tree.setParent(self)
            self.setRightChild(tree)

最后在生成的二叉查找树中进行搜索。

# 查找key值
# 递归
def find(self, data):
    if data == self.getKey():
        return self
    elif data < self.getKey() and self.getLeftChild():
        return self.getLeftChild().find(data)
    elif data > self.getKey() and self.getRightChild():
        return self.getRightChild().find(data)
    else:
        return None

# 非递归
def find1(self, data):
    while data != self.getKey():
        if data < self.getKey():
            self = self.getLeftChild()
        else:
            self = self.getRightChild()
    return self

优缺点：
优点： 相较于二分查找，能高效实现插入和删除操作。
缺点： 树有可能是不平衡的，最糟糕情况下时间复杂度退化为$O(N)$。

5.2 平衡树之2-3查找树

2-3树的其中一个基本定义:

一棵2-3查找树或为一颗空树，或由以下节点组成：

• 2-节点： 含有一个键和两条链接，左链接指向的2-3树中的键都小于该节点，右链接指向的2-3树中的键都大于该节点。
• 3-节点： 含有两个键和三条链接，左链接指向的2-3树中的键都小于该节点，中链接指向的2-3树中的键都位于该节点的两个键之间，右链接指向的2-3树中的键都大于该节点。

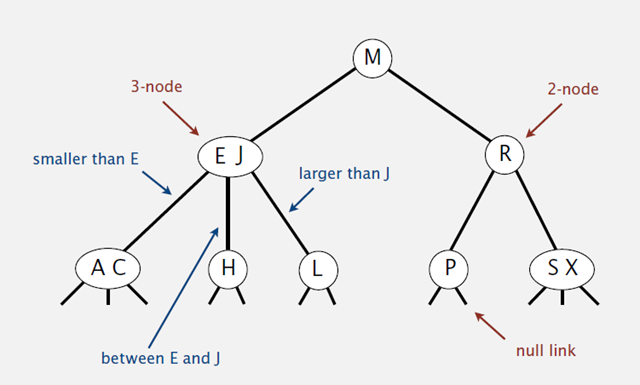
2-3查找树的性质：

• 任一节点只能是2度节点或3度节点，不存在元素数为0的节点。
• 2度节点：包含1个元素的节点将只能有2个子节点；
• 3度节点：包含2个元素的节点将只能有3个子节点；
• 所有叶子节点都拥有相同的深度（depth），即根节点到每一个为空节点的距离都相同。。
• 元素始终保持排序顺序。

相比二叉查找树，2-3树的优势：

• 2-3树可以获得更好的渐进查找时间$O(\log_2n)$。
• 2-3树更容易保持树的平衡。

复杂度分析： 2-3树的查找效率与树的高度是息息相关的。

• 在最坏的情况下，也就是所有的节点都是2-node节点，查找效率为$O(\log_2N)$
• 在最好的情况下，所有的节点都是3-node节点，查找效率为$O(\log_2 3N)$约等于$O(0.631\log_2N)$

优缺点：
优点： 2-3树在最坏情况下仍有较好的性能。每个操作中处理每个结点的时间都不会超过一个很小的常数，且这两个操作都只会访问一条路径上的结点，所以任何查找或插入的成本都不会超过对数级别。
缺点： 2-3树实现起来比较复杂。

5.3 平衡树之红黑树

基本思想： 红黑树的思想就是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

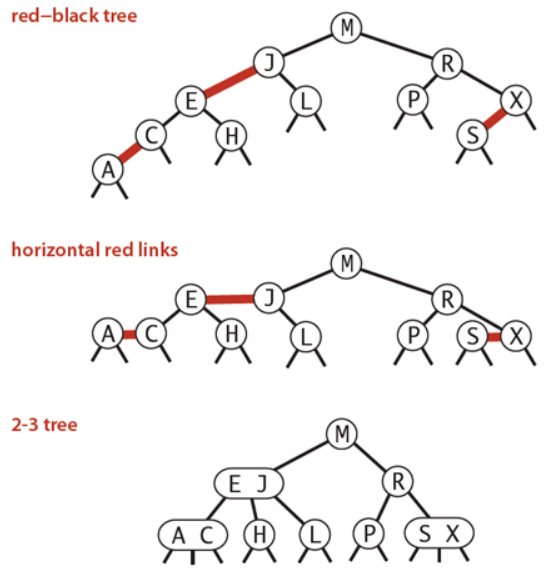
红黑树的定义： 红黑树是一种具有红色和黑色链接的平衡查找树，同时满足：

• 红色节点向左倾斜
• 一个节点不可能有两个红色链接
• 整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

红黑树的性质： 整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同，从根节点到叶子节点的距离都相等。

复杂度分析： 最坏的情况就是，红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。

注意： 红黑树的平均高度大约为$\log_2n$。

5.4 B树和B+树

6 分块查找

分块查找又称索引顺序查找，它是顺序查找的一种改进方法。
算法思想： 将$n$个数据元素”按块有序”划分为$m$块（$m\leq n$）。每一块中的结点不必有序，但块与块之间必须”按块有序”；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，依此类推。

算法流程：

1. 先选取各块中的最大关键字构成一个索引表；
2. 查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；
3. 然后，在已确定的块中用顺序法进行查找。

7 哈希查找

散列表（Hash table，也叫哈希表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

哈希表就是一种以键-值(key-indexed) 存储数据的结构，”直接定址“与”解决冲突“是哈希表的两大特点。

哈希函数的规则是：通过某种转换关系，使关键字适度的分散到指定大小的的顺序结构中，越分散，则以后查找的时间复杂度越小，空间复杂度越高。

算法思想： 哈希的思路很简单，如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。

算法流程：

1. 用给定的哈希函数构造哈希表；
2. 根据选择的冲突处理方法解决地址冲突； 常见的解决冲突的方法：拉链法和线性探测法。详细的介绍可以参见：浅谈算法和数据结构: 十一 哈希表。
3. 在哈希表的基础上执行哈希查找。

复杂度分析： 单纯论查找复杂度：对于无冲突的Hash表而言，查找复杂度为$O(1)$。

Hash是一种典型以空间换时间的算法，比如原来一个长度为100的数组，对其查找，只需要遍历且匹配相应记录即可，从空间复杂度上来看，假如数组存储的是byte类型数据，那么该数组占用100byte空间。现在我们采用Hash算法，我们前面说的Hash必须有一个规则，约束键与存储位置的关系，那么就需要一个固定长度的hash表，此时，仍然是100byte的数组，假设我们需要的100byte用来记录键与位置的关系，那么总的空间为200byte,而且用于记录规则的表大小会根据规则，大小可能是不定的。

# 除法取余法实现的哈希函数
def myHash(data, hashLength,):
    return data % hashLength

# 哈希表检索数据
def searchHash(hash, hashLength, data):
    hashAddress = myHash(data, hashLength)
   # 指定hashAddress存在，但并非关键值，则用开放寻址法解决
    while hash.get(hashAddress) and hash[hashAddress] != data:
        hashAddress += 1
        hashAddress = hashAddress % hashLength
    if hash.get(hashAddress) == None:
        return None
    return hashAddress

# 数据插入哈希表
def insertHash(hash, hashLength, data):
    hashAddress = myHash(data, hashLength)
    # 如果key存在说明应经被别人占用， 需要解决冲突
    while(hash.get(hashAddress)):
        # 用开放寻执法
        hashAddress += 1
        hashAddress = myHash(hashAddress, hashLength)
    hash[hashAddress] = data

if __name__ == '__main__':
    hashLength = 20
    L = [13, 29, 27, 28, 26, 30, 38, 47]
    hash = {}
    for i in L:
        insertHash(hash, hashLength, i)
    print('hash表内容：', hash)
    result = searchHash(hash, hashLength, 47)
    if result:
        print("数据已找到，索引位置在",result)
        print(hash[result])
    else:
        print("没有找到数据")
    
输出：
hash表内容： {13: 13, 9: 29, 7: 27, 8: 28, 6: 26, 10: 30, 18: 38, 11: 47}
数据已找到，索引位置在 11
47

参考文献

七大查找算法
常用查找算法
浅谈算法和数据结构: 八 平衡查找树之2-3树
平衡查找树（2-3-4 树）
浅谈算法和数据结构: 十一 哈希表