机器学习理论总结
1 方差与偏差
学习算法的预测误差, 或者说泛化误差(generalization error)可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise)。
\[Error = Bias + Variance + Noise\]在估计学习算法性能的过程中, 我们主要关注偏差与方差。因为噪声属于不可约减的误差 (irreducible error)。所以一个模型的好坏是根据偏差和方差来衡量的。
在训练集$D$上模型$f$对测试样本$x$的预测输出为$f(x;D)$,那么学习算法$f$对测试样本$x$的期望预测为:
上面的期望预测也就是针对不同数据集$D$,$f$对$x$的预测值取其期望,也被叫做 average predicted。
偏差:描述的是期望预测$\hat f(x)$与真实值$y$之间的差距。偏差越大,越偏离真实数据。
方差:描述的是预测值$f(x;D)$的变化范围,离散程度,是预测值的方差,也就是离其期望预测$\hat f(x)$的距离。方差越大,数据的分布越分散。
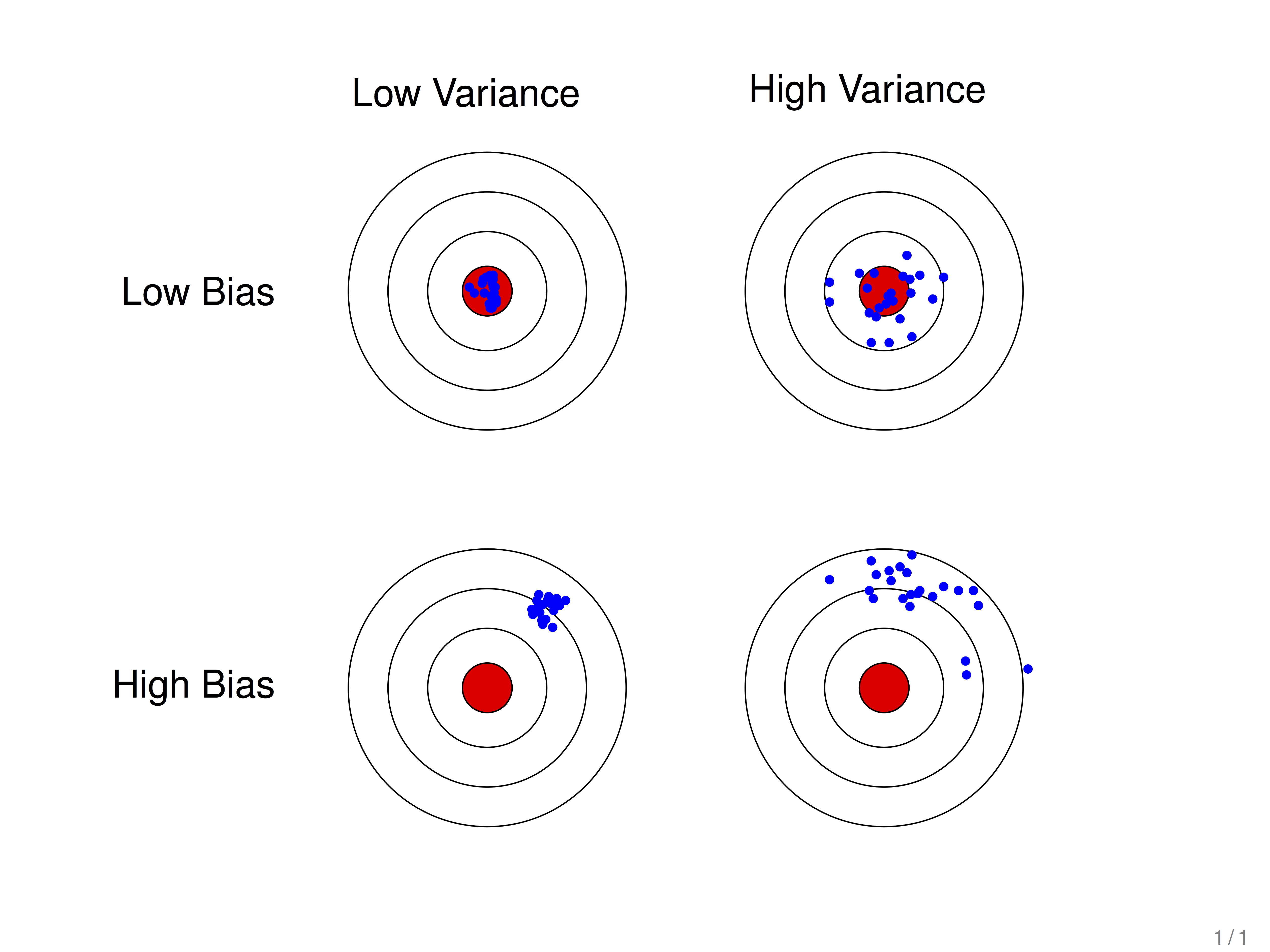
假设红色的靶心区域是学习算法完美的正确预测值,蓝色点为每个数据集所训练出的模型对样本的预测值,当我们从靶心逐渐向外移动时,预测效果逐渐变差。
很容易看出有两副图中蓝色点比较集中,另外两幅中比较分散,它们描述的是方差的两种情况。比较集中的属于方差小的,比较分散的属于方差大的情况。
再看蓝色点与红色靶心区域的位置关系,靠近红色靶心的属于偏差较小的情况,远离靶心的属于偏差较大的情况。
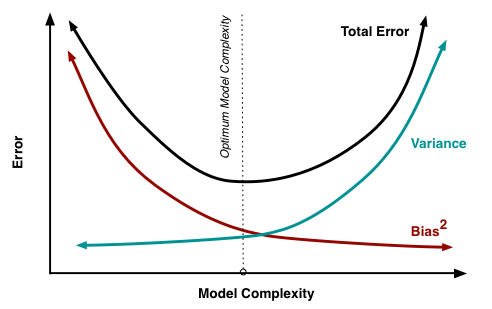
随着模型复杂度的提升,偏差逐渐减小,方差逐渐增大。
2 过拟合欠拟合问题
如果学习算法不如预期,基本上是由两个原因造成:
- 高偏差:训练误差大,验证误差大。即欠拟合。
- 高方差:训练误差小,验证误差大。即过拟合。
2.1 多项式回归中偏差与方差
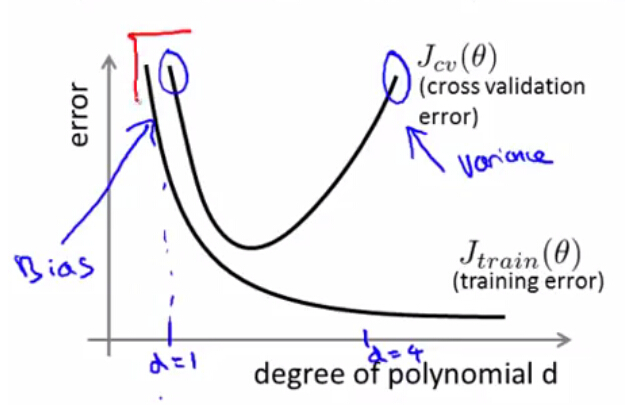
在多项式回归中,如果多项式次数较高,则容易造成过拟合,此时训练误差很低,但是对于新数据的泛化能力较差,导致交叉验证集和测试集的误差都很高,此时模型出现了高方差。而当次数较低时,又易出现欠拟合的状况,此时无论是训练集,交叉验证集,还是测试集,都会有很高的误差,此时模型出现了高偏差。
2.2 正规化过程的偏差与方差
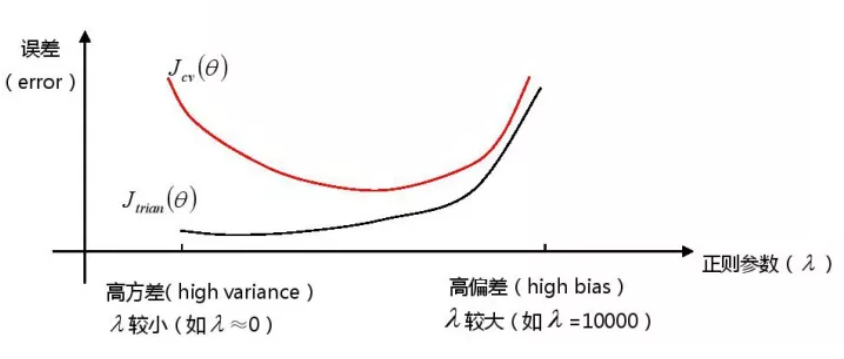
正规化(Regularization)能帮我们解决过拟合问题,$\lambda$取值越大,对参数$\theta$的惩罚力度就越大,能够帮助解决过拟合问题,但是,如果惩罚过重,也会造成欠拟合问题,即会出现高偏差。如果$\lambda$取值较小,则意味着没有惩罚$\theta$,也就不能解决过拟合问题,会出校高方差。
2.3 样本数目对与偏差方差的影响
当样本数目$m$很小时,模型很容易拟合数据,因而误差很小,近乎为0;随着训练集数据的增加,即使再完美的模型也无法100%拟合数据,因而随着数据量的增加,未被拟合的数据也会相对增多,即误差逐渐增多。
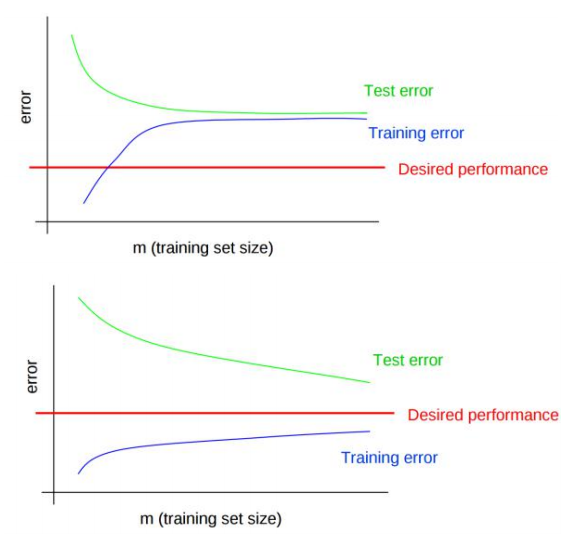
- 对于高偏差模型(上图第一个),训练误差和验证误差很接近,但都处于很大的误差水平之上。此时,无论怎么增加训练集数目,都无法降低误差。
- 对于高方差模型(上图第二个),训练误差在很低的水平,但是验证误差和训练误差的缺口很大,此时增加训练集样本数目,可以使得验证误差更接近训练误差。即当模型出现高方差问题,可以通过增加样本数目来降低方差。
2.4 解决方法
- 解决欠拟合:
- 增加特征个数
$n$; - 增加多项式阶数
$d$; - 减小正则项参数值
$\lambda$; - Boosting ,Boosting 往往会有较小的 Bias,比如 Gradient Boosting等。
- 增加特征个数
- 解决过拟合:
- 减少特征个数
$n$; - 减少多项式阶数
$d$; - 增加正则项参数值
$\lambda$; - 增加训练集样本
$m$; - Bagging ,将多个弱学习器Bagging 一下效果会好很多,比如随机森林等。
- 减少特征个数
3 L1正则化和L2正则化
参见:
L1正则化:是指权值向量$w$中各个元素的绝对值之和,通常表示为$||w||_1$
L2正则化:是指权值向量$w$中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为$||w||_2$
作用:
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择(权重为0表示对应的特征没有作用,被丢掉),也可以增强模型可解释性(例如研究影响疾病的因素,只有少数几个非零元素,就可以知道这些对应的因素和疾病相关)
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
