动态查找树主要有：二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree），红黑树(Red-Black Tree )，B-tree/B+-tree/B*-tree(B~Tree) 。前三者是典型的二叉查找树结构，其查找的时间复杂度$O(\log_2N)$与树的深度相关，那么降低树的深度自然会提高查找效率。

一个实际问题：就是大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的（如果元素数量非常多的话，查找就退化成节点内部的线性查找了），这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下，那么如何减少树的深度（当然是不能减少查询的数据量），一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）。

1 B 树

B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以$O(\log_2 n)$的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同，B树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。
B树又叫平衡多路查找树。一棵$m$阶的B树的特性如下：

1. 树中每个结点至多有$m$个孩子；
2. 除根结点和叶子结点外，其它每个结点至少有$[ceil(m/2)]$个孩子（其中$ceil(x)$是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null，这里是将null结点作为叶子结点)；
5. 每个非终端结点中包含有$n$个关键字信息：$(n,P_0,K_1,P_1,K_2,P_2,...,K_n,P_n)$。其中：
   • $K_i(i=1...n)$为关键字，且关键字按顺序升序排序$K_{i-1}<K_i$。
   • $P_i$为指向子树根的接点，且指针$P_{i-1}$指向子树种所有结点的关键字均小于$K_i$，但都大于$K_{i-1}$。
   • 关键字的个数$n$必须满足：$[ceil(m/2)-1]\leq n\leq m-1$。
6. 如果一个非叶节点有$N$个子节点，则该节点的关键字数等于$N-1$；

下图是一个$m=3$阶B树：

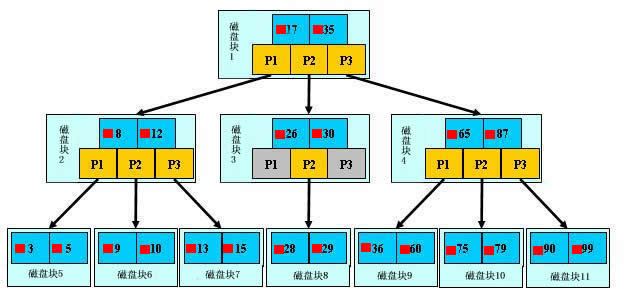
2 B+ 树

B+ 树是一种树数据结构，通常用于数据库和操作系统的文件系统中。B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度$O(\log_2 n)$。B+ 树元素自底向上插入，这与二叉树恰好相反。

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。

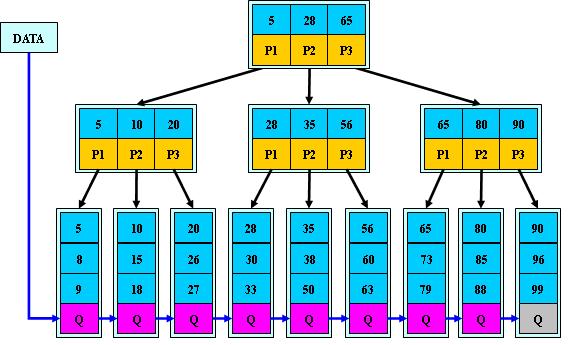
一棵$m$阶的B+ 树和$m$阶的B 树的差异在于：

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
2. 不可能在非叶子结点命中；
3. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
4. 更适合文件索引系统。

3 B* 树

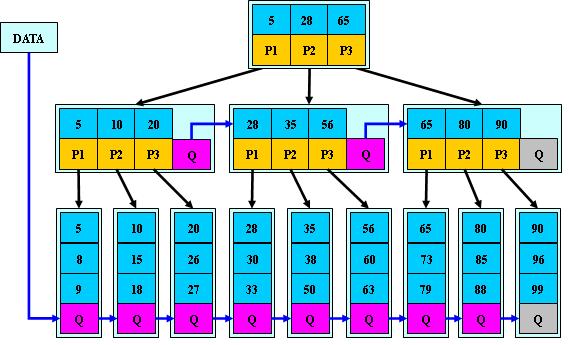
参考文献

从B树、B+树、B*树谈到R 树
平衡二叉树、B树、B+树、B*树 理解其中一种你就都明白了
B-树 B+树
B树——维基百科
B+ 树——维基百科