1 XGBoost

XGBoost 的目标函数由损失函数和复杂度组成。复杂度又由叶子数量和 L2 正则组成。

\[Obj(\Theta)=\sum\limits_il(y_i, \hat y_i)+\sum\limits_k\Omega(f_k) \\ \Omega(f)=\gamma T+\dfrac{1}{2}\lambda||w||^2\]

其中$i$是样本id，$k$是树id（轮数），$T$是叶子结点的总数，由于loss函数和复杂度项都是凸函数，所以有最小值。$w$是给定了某个输入对应每个叶子结点分数是什么，将$w$的$L_2$正则项加在目标函数中，可以有效的防止过拟合。叶子节点的数目也作为正则项加在了目标函数中，一定程度上限制了叶子数量，防止过拟合。而传统GBDT防止过拟合的手段是预剪枝或者后剪枝。

XGBoost的具体推导过程参见XGBoost 与 Boosted Tree和XGBoost 介绍。

XGBoost的步骤：

1. 对loss function进行二阶Taylor Expansion，展开以后的形式里，当前待学习的Tree是变量，需要进行优化求解。
2. Tree的优化过程，包括两个环节：
   • 枚举每个叶结点上的特征潜在的分裂点
   • 对每个潜在的分裂点，计算如果以这个分裂点对叶结点进行分割以后，分割前和分割后的loss function的变化情况。

因为Loss Function满足累积性，并且每个叶结点对应的weight的求取是独立于其他叶结点的（只跟落在这个叶结点上的样本有关），所以，不同叶结点上的loss function满足单调累加性，只要保证每个叶结点上的样本累积loss function最小化，整体样本集的loss function也就最小化了。

XGBoost对GBDT的改进：

1. 避免过拟合： 目标函数之外加上了正则化项整体求最优解，用以权衡目标函数的下降和模型的复杂程度，避免过拟合。基学习为CART时，正则化项与树的叶子节点的数量T和叶子节点的值有关。
2. 使用二阶的泰勒展开精度更高： 不同于传统的GBDT只利用了一阶的导数信息的方式，XGBoost对损失函数做了二阶的泰勒展开，精度更高。
3. 树节点分裂优化： 选择候选分割点针对GBDT进行了多个优化。正常的树节点分裂时公式如下：
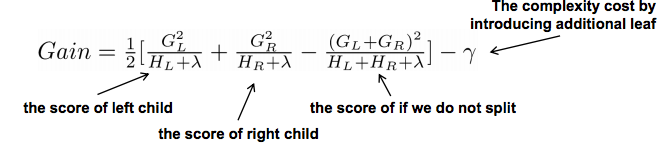
   这个公式形式上跟ID3算法（采用信息熵计算增益）或者CART算法（采用基尼指数计算增益） 是一致的，都是用分裂后的某种值减去分裂前的某种值，从而得到增益。我们可以加入阈值，当增益大于阈值时才让节点分裂，上式中的γ即阈值，它是正则项里叶子节点数T的系数，所以xgboost在优化目标函数的同时相当于做了预剪枝。另外，上式中还有一个系数λ，是正则项里leaf score的L2模平方的系数，对leaf score做了平滑，也起到了防止过拟合的作用，这个是传统GBDT里不具备的特性。

缺点：

• 在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。
• 预排序方法（pre-sorted）：首先，空间消耗大。这样的算法需要保存数据的特征值，还保存了特征排序的结果（例如排序后的索引，为了后续快速的计算分割点），这里需要消耗训练数据两倍的内存。其次时间上也有较大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。
• 对cache优化不友好。在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对cache进行优化。同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的cache miss。

2 LightGBM

LightGBM是个快速的、分布式的、高性能的基于决策树算法的梯度提升框架。可用于排序、分类、回归以及很多其他的机器学习任务中。

它采用最优的leaf-wise(按叶子生长)策略分裂叶子节点，然而其它的提升算法分裂树一般采用的是depth-wise或者level-wise(按层生长)而不是leaf-wise。

Leaf-Wise分裂导致复杂性的增加并且可能导致过拟合。但是这是可以通过设置另一个参数 max-depth 来克服，它分裂产生的树的最大深度。

LightGBM的优势:

1. 更快的训练速度和更高的效率：LightGBM使用基于直方图的算法。例如，它将连续的特征值分桶(buckets)装进离散的箱子(bins)，这是的训练过程中变得更快。
2. 更低的内存占用：使用离散的箱子(bins)保存并替换连续值导致更少的内存占用。
3. 更高的准确率(相比于其他任何提升算法) ：它通过leaf-wise分裂方法产生比level-wise分裂方法更复杂的树，这就是实现更高准确率的主要因素。然而，它有时候或导致过拟合，但是我们可以通过设置 max-depth 参数来防止过拟合的发生。
4. 大数据处理能力：相比于XGBoost，由于它在训练时间上的缩减，它同样能够具有处理大数据的能力。
5. 支持并行学习

LightGBM的优化:

1. 基于Histogram(直方图)的决策树算法
2. 带深度限制的Leaf-wise的叶子生长策略，大大提升了速度和精度
3. 直方图做差加速
4. 直接支持类别特征(Categorical Feature)
5. Cache命中率优化
6. 基于直方图的稀疏特征优化
7. 多线程优化
8. 实现了特征并行、数据并行和投票并行

2.1 Histogram算法

直方图算法的基本思想：先把连续的浮点特征值离散化成$k$个整数，同时构造一个宽度为$k$的直方图。遍历数据时，根据离散化后的值作为索引在直方图中累积统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。

优点： 首先，最明显就是内存消耗的降低，直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用8位整型存储就足够了，内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低，预排序算法每遍历一个特征值就需要计算一次分裂的增益，而直方图算法只需要计算k次（k可以认为是常数），时间复杂度从O(#data*#feature)优化到O(k*#features)。

缺点： 由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。

2.2 带深度限制的Leaf-wise的叶子生长策略

Level-wise过一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。但实际上Level-wise是一种低效算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。

Leaf-wise则是一种更为高效的策略：每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。

Leaf-wise的缺点：可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度限制，在保证高效率的同时防止过拟合。

3 总结

3.1 GBDT和XGBoost的区别

参考XGBoost浅入浅出。

Boosting的思想是每一个基分类器纠正前一个基分类器的错误，至于纠正的方式不同所以有不同的Boosting算法，比如通过调整样本权值分布训练基分类器对应的AdaBoost，通过拟合前一个基分类器与目标值的误差的负梯度(也不能说是残差，只有在损失函数是平方损失时才能叫残差，一般的损失函数是近似残差)来学习下一个基分类器的方法是Gradient Boosting。

Adaboost是前向分布算法+指数损失函数，GBDT是前向分布算法在较难优化的损失函数情况时的一种近似的优化，用损失函数的负梯度作为残差的近似值，用到泰勒一阶展开，XGBoost支持任意损失函数，只要一阶二阶可导即可，用到泰勒二阶展开。

1. 传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。
2. 传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导。
3. xgboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的$L_2$模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是xgboost优于传统GBDT的一个特性。
4. 列抽样（column subsampling）。xgboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。
5. xgboost工具支持并行。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

3.2 集成学习家谱关系图

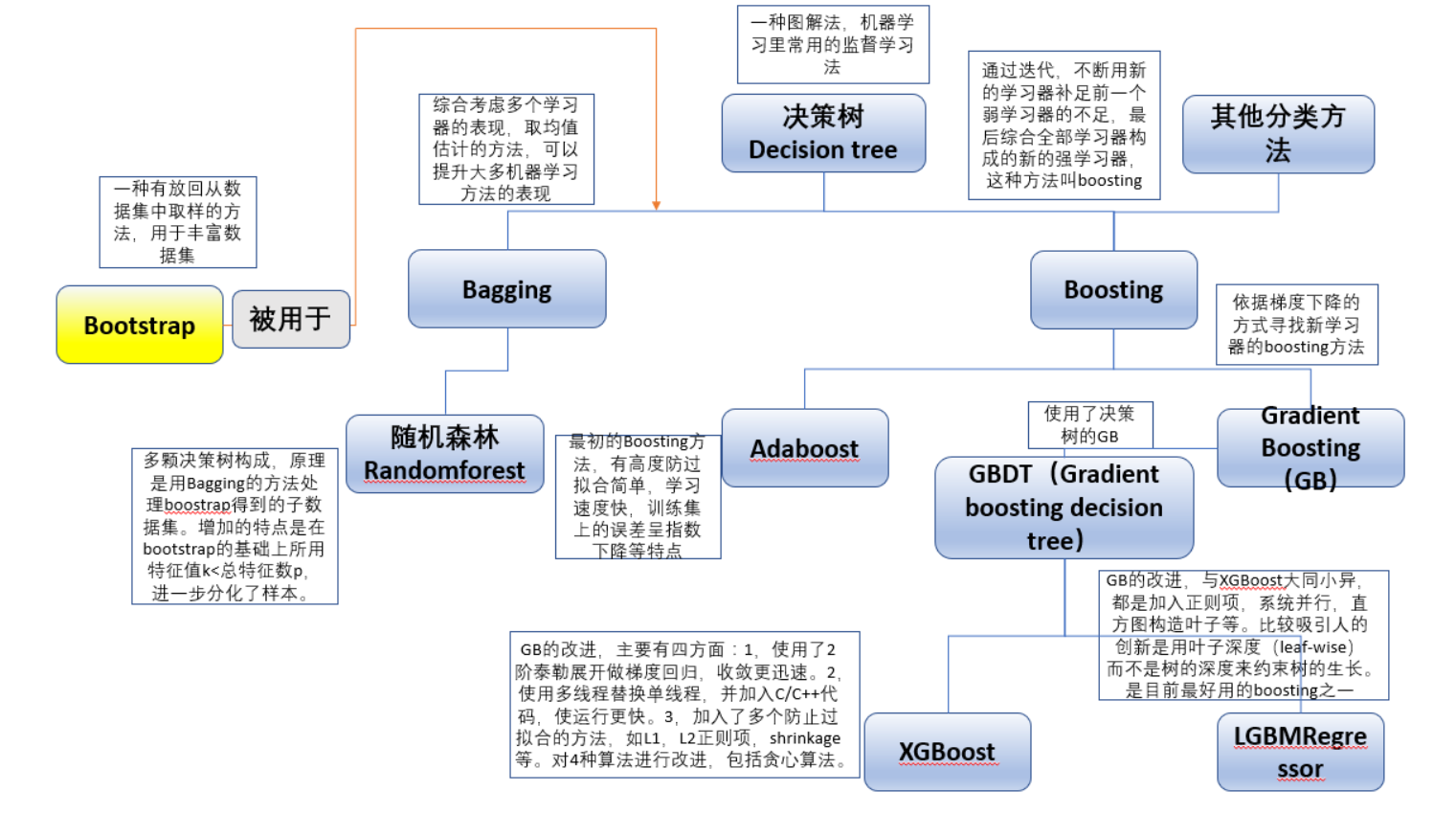
参考文献

XGBoost 与 Boosted Tree
XGBoost 介绍
机器学习算法系列（8）：XgBoost
XGBoost浅入浅出
xgboost详解
LightGBM大战XGBoost，谁将夺得桂冠？
lightGBM原理、改进简述
开源 | LightGBM：三天内收获GitHub 1000 星
决策树及其主要Ensemble算法的区别和联系