Morris Traversal遍历二叉树

2019-01-05

数据结构与算法

通常我们遍历一棵二叉树，可以用前序、中序或后序的方法来遍历，同时可以采取迭代或者递归的方法，然而这两种方法的时间和空间复杂度都是 $O(n)$ 。

而Morris Traversal方法可以做到以下两条：

可以在 $O(1)$ 的空间复杂度下，同样在 $O(n)$ 的时间复杂度下完成遍历。
二叉树的形状没有被破坏（中间过程允许改变其形状）。

Morris方法用到了线索二叉树的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱和后继节点，只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。
其中二叉树的结构如下：

class BinaryTree(object):
    def __init__(self, data):
        self.__key = data
        self.__leftChild = None
        self.__rightChild = None

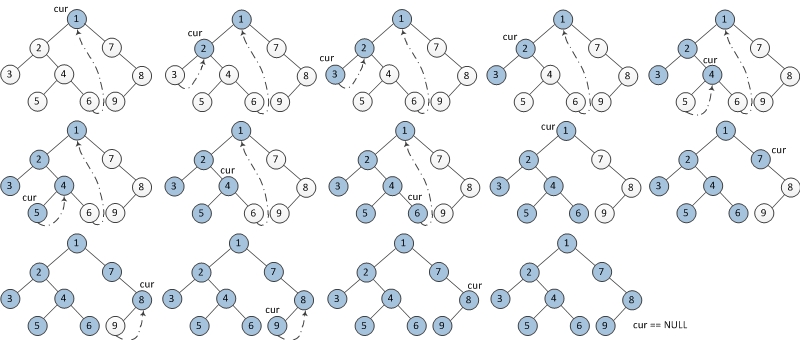
1 先序遍历

如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。
如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
- 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。输出当前节点（在这里输出，这是与中序遍历唯一一点不同）。当前节点更新为当前节点的左孩子。
- 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。当前节点更新为当前节点的右孩子。
重复以上1、2直到当前节点为空

先序图示

def preOrderByMorris(self, root, nodelist = None):
        if not nodelist:
            nodelist = []
        cur = root
        pre = None
        while cur:
            if not cur.getLeft():
                nodelist.append(cur.getKey())
                cur = cur.getRight()
            else:
                # 在当前节点的左子树中找到当前节点在中序遍历下的前驱节点
                pre = cur.getLeft()
                while pre.getRight() and pre.getRight() != cur:
                    pre = pre.getRight()
                if not pre.getRight():
                    pre.setRight(cur)
                    nodelist.append(cur.getKey())
                    cur = cur.getLeft()
                elif pre.getRight() == cur:
                    pre.setRight(None)
                    cur = cur.getRight()
        return nodelist

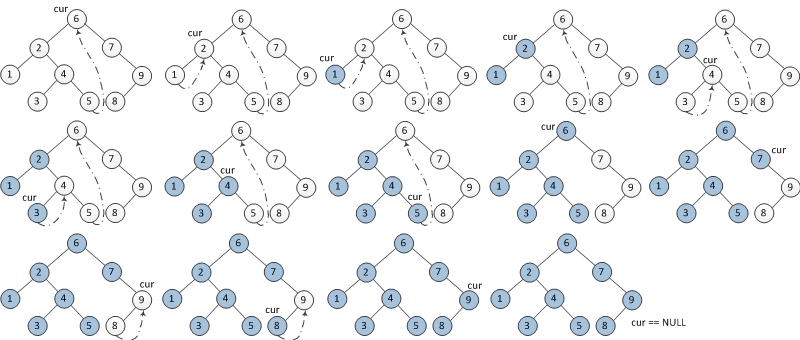
2 中序遍历

如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。
如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
- 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
- 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空（恢复树的形状）。输出当前节点，当前节点更新为当前节点的右孩子。
重复以上1、2直到当前节点为空。

中序图示

def inOrderByMorris(self, root, nodelist = None):
        if not nodelist:
            nodelist = []
        cur = root
        pre = None
        while cur:
            if not cur.getLeft():
                nodelist.append(cur.getKey())
                cur = cur.getRight()
            else:
                # 在当前节点的左子树中找到当前节点在中序遍历下的前驱节点
                pre = cur.getLeft()
                while pre.getRight() and pre.getRight() != cur:
                    pre = pre.getRight()
                if not pre.getRight():
                    pre.setRight(cur)
                    cur = cur.getLeft()
                elif pre.getRight() == cur:
                    pre.setRight(None)
                    nodelist.append(cur.getKey())
                    cur = cur.getRight()
        return nodelist

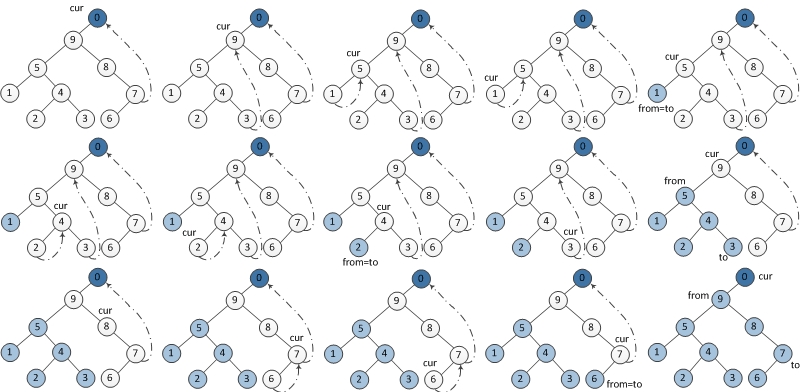
3 后序遍历

后续遍历比较复杂一点，需要建立一个临时节点dump，令其左孩子是root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。

当前节点设置为临时节点dump。
如果当前节点的左孩子为空，则将其右孩子作为当前节点。
如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
- 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
- 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右孩子。
重复以上2、3直到当前节点为空。

后序图示

def postOrderByMorris(self, root, nodelist = None):
        if not nodelist:
            nodelist = []
        dump = BinaryTree(-1)  # 初始化一个临时节点
        dump.setLeft(root)
        cur = dump
        pre = None
        while cur:
            if not cur.getLeft():
                cur = cur.getRight()
            else:
                # 在当前节点的左子树中找到当前节点在中序遍历下的前驱节点
                pre = cur.getLeft()
                while pre.getRight() and pre.getRight() != cur:
                    pre = pre.getRight()
                if not pre.getRight():
                    pre.setRight(cur)
                    cur = cur.getLeft()
                elif pre.getRight() == cur:
                    pre.setRight(None)
                    # 倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点
                    tmp = self.reversePrint(cur.getLeft(), pre)
                    nodelist.extend(tmp)  # extend函数完成list的拼接，没有返回值
                    cur = cur.getRight()
        return nodelist

def reversePrint(self, fromNode, toNode):
    tmp = []  # 用于存储顺序访问的值
    node = fromNode
    while node != toNode.getRight():
        tmp.append(node.getKey())
        node = node.getRight()
    tmp.reverse()  # reverse函数没有返回值
    return tmp

 LRU算法二叉树的遍历 