逻辑回归(分类)
1 概述
逻辑回归属于判别式模型,相比于线性回归,逻辑回归只会输出一些离散的特定值(例如判定一封邮件是否为垃圾邮件,输出只有 0 和 1 ),而且对假设函数进行了处理,使得输出只在 0 和 1 之间。逻辑回归虽然名字叫回归,但实际上它是一个分类算法。它不仅可以预测出类别,还可以输出近似概率预测。
假设函数:$h_\theta(x)=g(\theta^TX)$
其中$X$代表特征向量,$g$代表逻辑函数,是一个常用的S形函数(sigmoid function),公式是:$g(z)=\dfrac{1}{1+e^{-z}}$
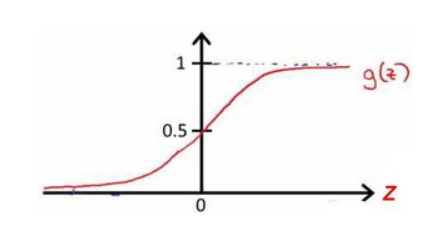
$h_\theta(x)$的作用是,对于给定的输入变量,根据选择的参数计算输出变量等于1的可能性(estimated probablity),即 $h_\theta(x)=P(y=1|x;\theta)$。 例如,如果对于给定的 $x$,通过已经确定的参数计算得出$h_\theta(x)=0.7$,则表示有70%的几率为 $y$ 正向类,相应地为 $y$ 负向类的几率为$1-0.7=0.3$。
在逻辑回归中,我们预测:
当$h_\theta(x)>=0.5$时,预测$y=1$。
当$h_\theta(x)<0.5$时,预测$y=0$。
根据上面绘制出的 S 形函数图像,我们知道当:
$z=0$时,$g(z)=0.5$;
$z>0$时,$g(z)>0.5$;
$z<0$时,$g(z)<0.5$。
又$z=\theta^TX$,即:$\theta^TX>=0$时,预测$y=1$;$\theta^TX<0$时,预测$y=0$。
代价函数: $J(\theta)=\dfrac{1}{m}\sum\limits_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$,其中:
$Cost(h_\theta(x),y)= \begin{cases}-log(h_\theta(x))&if&y=1\\-log(1-h_\theta(x))&if&y=0\end{cases}$
将构建的$Cost(h_\theta(x),y)$简化如下:
$Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))$
再将上式带入代价函数可以得到:
$J(\theta)=\dfrac{1}{m}\sum\limits_{i=1}^m-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))$
即:
$J(\theta)=-\dfrac{1}{m}\sum\limits_{i=1}^my^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))$
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。
2 总结
优点:
- 实现简单,广泛的应用于工业问题上;
- 分类时计算量非常小,速度很快,存储资源低;
- 便利的观测样本概率分数;
- 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题。
缺点:
- 当特征空间很大时,逻辑回归的性能不是很好;
- 容易欠拟合,一般准确度不太高;
- 不能很好地处理大量多类特征或变量;
- 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分;
- 对于非线性特征,需要进行转换。
