1 贝叶斯定理

贝叶斯定理是关于随机事件$A$和$B$的条件概率的一则定理。
所谓的条件概率就是指在事件$B$发生的情况下，事件$A$发生的概率，用$P(A|B)$来表示。

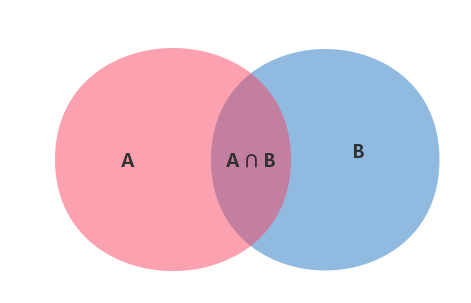
根据文氏图，可以很清楚地看到在事件$B$发生的情况下，事件$A$发生的概率就是$P(A \cap B)$除以$P(B)$。
$P(A|B)=\dfrac{P(A \cap B)}{P(B)}$
因此：$P(A \cap B)=P(A|B)P(B)$
同理可得：$P(A \cap B)=P(B|A)P(A)$
所以：$P(A|B)P(B)=P(B|A)P(A)$
即：$P(A|B)=\dfrac{P(B|A)P(A)}{P(B)}$

2 全概率公式

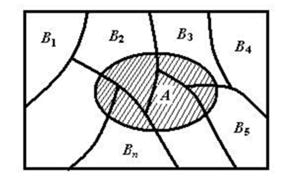
假设$\{B_n:n=1,2,3,...\}$ 是一个概率空间的有限或者可数无限的分割（既 $B_n$为一完备事件组），且每个集合$B_n$是一个可测集合，则对任意事件$A$有全概率公式：
$P(A)=\sum\limits_{i=1}^nP(A \cap B_n)$
又因为：$P(A \cap B_n)=P(A|B_n)P(B_n)$，所以全概率公式可以写作为：
$P(A)=\sum\limits_{i=1}^nP(A|B_n)P(B_n)$
全概率公式将对一复杂事件$A$的概率求解问题转化为了在不同情况或不同原因$B_n$下发生的简单事件的概率的求和问题。

3 朴素贝叶斯分类

朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。
通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的定义如下：

1. 设$x=\{a_1,a_2,...,a_m\}$为一个待分类项，而每个$a$为$x$的一个特征属性。
2. 有类别集合$C=\{y_1,y_2,...,y_n\}$。
3. 计算$P(y_1|x),P(y_2|x),...,P(y_n|x)$。
4. 如果$P(y_k|x)=max\{P(y_1|x),P(y_2|x),...,P(y_n|x)\}$，则$x\in y_k$。

其中第3步中的计算如下：

\[P(y_i|x)=\dfrac{P(x|y_i)P(y_i)}{P(x)} =\dfrac{P(a_1|y_i)P(a_2|y_i)...P(a_m|y_i)P(y_i)}{P(x)}\]

由于分母对于所有类别都为常数，所以可以忽略不记。所以可得：

\[P(y_i|x)=P(x|y_i)P(y_i)=P(a_1|y_i)P(a_2|y_i)...P(a_m|y_i)P(y_i)\]

4 总结

优点：

• 朴素贝叶斯模型发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。
• 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练；
• 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

• 需要计算先验概率；
• 分类决策存在错误率；
• 对输入数据的表达形式很敏感。

参考文献

贝叶斯推断及其互联网应用（一）：定理简介
算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)