数据结构——平衡二叉搜索树
平衡二叉搜索树(英语:Balanced Binary Tree)是一种结构平衡的二叉搜索树,即叶节点高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。它能在$O(\log_2n)$内完成插入、查找和删除操作,最早被发明的平衡二叉搜索树为AVL树。
常见的平衡二叉搜索树有:AVL树、红黑树和Treap(树堆)。
1 AVL树
它是最先发明的自平衡二叉查找树,也被称为高度平衡树。相比于”二叉查找树”,它的特点是:AVL树中任何节点的两个子树的高度最大差别为1。
注意: 树的高度为最大层次。即空的二叉树的高度是0,非空树的高度等于它的最大层次(根的层次为1,根的子节点为第2层,依次类推)。
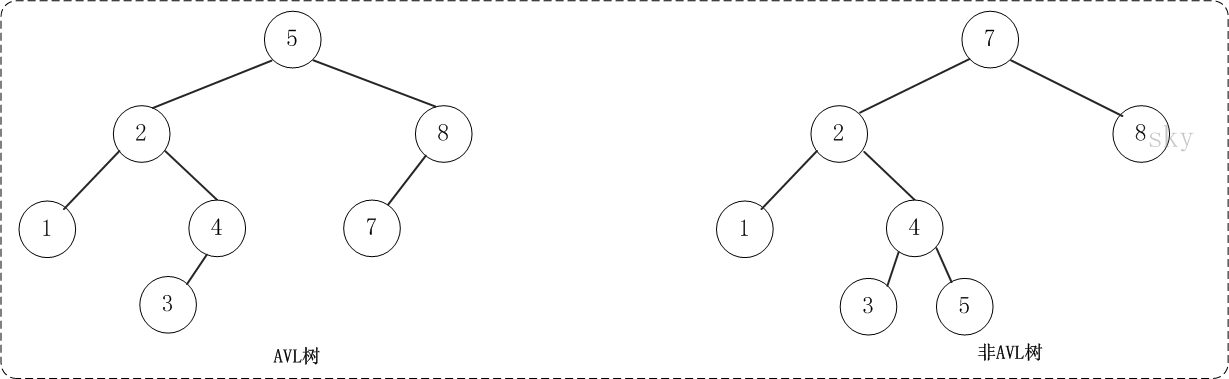
上面这张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1;而右边的不是AVL树,因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3,而以8为根节点的树的高度是1)。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子-2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
1.1 代码实现
1.1.1 AVL树的定义
class AVLTree(object):
def __init__(self,key):
self.key=key # 该结点的值
self.left=None
self.right=None
self.height=0 # 该结点的高度
1.1.2 查找
# 查找某个值
def find(self,data):
if data == self.key:
return self
elif data < self.key and self.left:
return self.left.find(data)
elif data > self.key and self.right:
return self.right.find(data)
else:
return None
1.1.3 获取最大最小结点
# 返回树中的最小元素与最大元素的结点
def findMin(self):
if self.left:
return self.left.findMin()
else:
return self
def findMax(self):
tree = self
if tree:
while tree.right:
tree = tree.right
return tree
1.1.4 获取节点高度
该程序中定义的是树的叶子结点高度为0,空结点的高度为-1。
# 计算结点的高度
def getNodeHeight(self, node):
if node is None:
return -1
else:
return node.height
1.1.5 旋转结点
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。我们需要找出第一个破坏了平衡条件的节点,称之为$K$。$K$的两颗子树的高度差2。这种失去平衡的可以概括为4种情况:LL(左左),LR(左右),RR(右右)和RL(右左)。
- LL: 对
$K$的左孩子的左子树进行插入或删除一个节点后,$K$的左孩子的左子树还有非空子节点。 - LR: 对
$K$的左孩子的右子树进行插入或删除一个节点后,$K$的左孩子的右子树还有非空子节点。 - RR: 对
$K$的右孩子的右子树进行插入或删除一个节点后,$K$的右孩子的右子树还有非空子节点。 - RL: 对
$K$的右孩子的左子树进行插入或删除一个节点后,$K$的右孩子的左子树还有非空子节点。
情况1与3是对称的,需要进行一次单旋转操作,清况2与4需要一次双旋转操作。下面给出它们的示意图:


以下图表以四列表示四种情况,每行表示在该种情况下要进行的操作。在左左和右右的情况下,只需要进行一次旋转操作;在左右和右左的情况下,需要进行两次旋转操作。
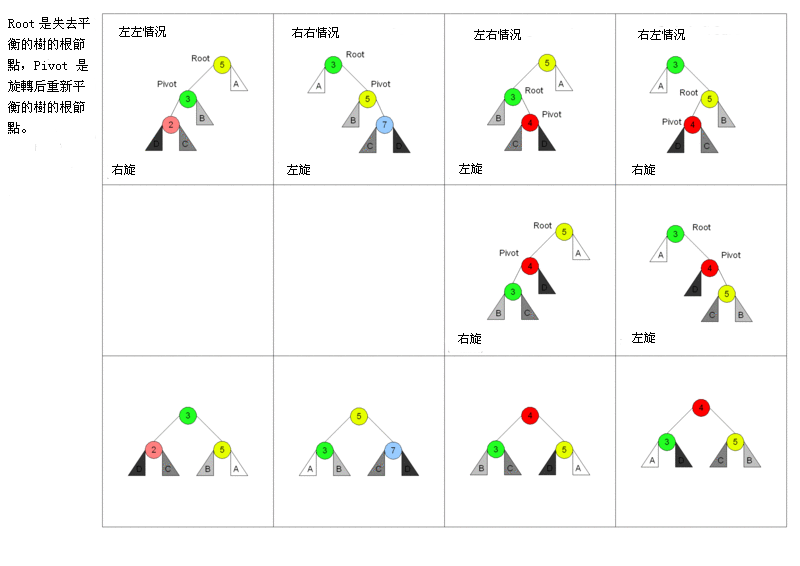
上图中我们看到旋转操作的核心是左旋和右旋两种操作,左旋和右旋互为逆操作。
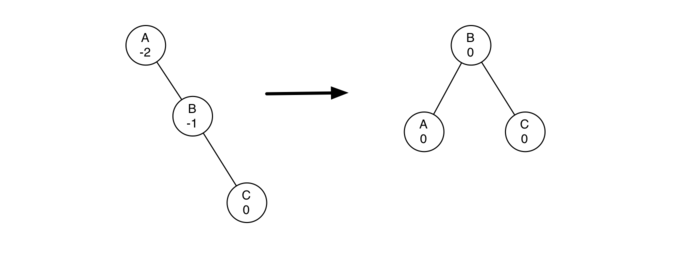
- 左旋:
- 提升右孩子(B)成为子树的根。
- 将旧根(A)移动为新根的左子节点。
- 如果新根(B)已经有一个左孩子,那么使它成为新左孩子(A)的右孩子。注意:由于新根(B)是A的右孩子,A的右孩子在这一点上保证为空。这允许我们添加一个新的节点作为右孩子。
# 左旋操作 def leftrotation(self, k): newRoot = k.right k.right = newRoot.left newRoot.left = k k.height = max(self.getNodeHeight(k.right), self.getNodeHeight(k.left)) + 1 newRoot.height = max(self.getNodeHeight(newRoot.right), k.height) + 1 return newRoot - 右旋:
- 提升左子节点(A)为子树的根。
- 将旧根(B)移动为新根的右子树。
- 如果新根(A)已经有一个右孩子,那么使它成为新右孩子(B)的左孩子。注意:由于新根(A)是B的左子节点,B的左子节点在此时保证为空。这允许我们添加一个新节点作为左孩子。
# 右旋操作 def rightrotation(self, k): newRoot = k.left k.left = newRoot.right newRoot.right = k k.height = max(self.getNodeHeight(k.right), self.getNodeHeight(k.left)) + 1 newRoot.height = max(self.getNodeHeight(newRoot.left), k.height) + 1 return newRoot
下面详细介绍具体的旋转操作:
-
LL的旋转:
LL失去平衡的情况,可以通过一次右旋让AVL树恢复平衡。如下图:
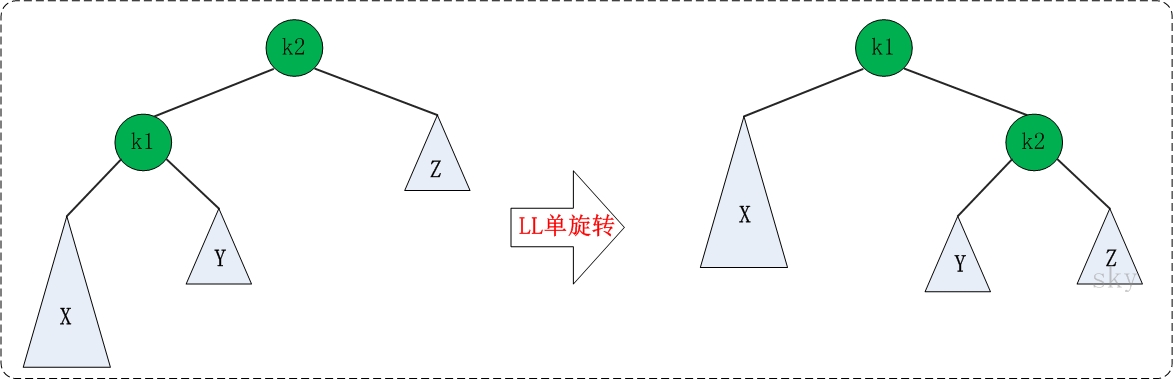
# LL操作 def left_left_rotation(self, k): return self.rightrotation(k) -
RR的旋转:
RR失去平衡的情况,可以通过一次左旋让AVL树恢复平衡。如下图:
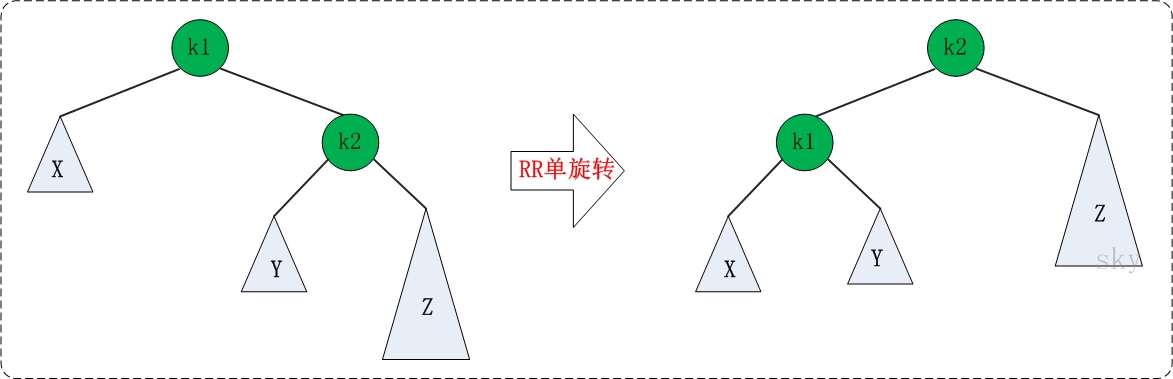
# RR操作 def right_right_rotation(self, k): return self.leftrotation(k) -
LR的旋转:
LR失去平衡的情况,可以通过一次左旋,然后在通过一次右旋让AVL树恢复平衡。如下图:

第一次旋转是围绕”k1”进行的”RR旋转”,第二次是围绕”k3”进行的”LL旋转”。# LR操作 def left_right_rotation(self, k): k.left = self.leftrotation(k.left) return self.rightrotation(k) -
RL的旋转: RL失去平衡的情况,可以通过一次右旋,然后在通过一次左旋让AVL树恢复平衡。如下图:

第一次旋转是围绕”k3”进行的”LL旋转”,第二次是围绕”k1”进行的”RR旋转”。# RL操作 def right_left_rotation(self, k): k.right = self.rightrotation(k.right) return self.leftrotation(k)
1.1.6 插入结点
# 插入结点操作
def insertoption(self, data, curNode):
if curNode is None:
curNode = AVLTree(data)
elif data < curNode.key:
curNode.left = self.insertoption(data, curNode.left)
# 插入节点后,若AVL树失去平衡,则进行相应的调节。
if self.getNodeHeight(curNode.left) - self.getNodeHeight(curNode.right) == 2:
if data < curNode.left.key:
curNode = self.left_left_rotation(curNode)
else:
curNode = self.left_right_rotation(curNode)
elif data > curNode.key:
curNode.right = self.insertoption(data, curNode.right)
# 插入节点后,若AVL树失去平衡,则进行相应的调节。
if self.getNodeHeight(curNode.right) - self.getNodeHeight(curNode.left) == 2:
if data < curNode.right.key:
curNode = self.right_left_rotation(curNode)
else:
curNode = self.right_right_rotation(curNode)
curNode.height = max(self.getNodeHeight(curNode.right), self.getNodeHeight(curNode.left)) + 1
return curNode
1.1.7 删除结点
删除操作比较复杂,具体如下。
- 先递归查找要删除的结点
- 当前节点为要删除的节点且有左子树右子树
- 如果右子树高度较高,则从右子树选取最小节点,将其值赋予当前节点,然后删除右子树的最小节点。这样操作当前节点的平衡不会被破坏。
- 如果左子树高度较高,则从左子树选取最大节点,将其值赋予当前节点,然后删除左子树的最大节点。这样操作当前节点的平衡不会被破坏。
- 当前节点为要删除的节点且是树叶(无子树),直接删除,当前节点(为None)的平衡不受影响。
- 当前节点为要删除的节点且只有一个左儿子或右儿子,用左儿子或右儿子代替当前节点,当前节点的平衡不受影响。
# 删除操作
def deleteoption(self, data, curNode):
if curNode is None:
print('AVL树中不存在该值的结点')
raise KeyError
elif data < curNode.key:
curNode.left = self.deleteoption(data, curNode.left)
if self.getNodeHeight(curNode.right) - self.getNodeHeight(curNode.left) == 2:
tmp = curNode.right
if self.getNodeHeight(tmp.left) > self.getNodeHeight(tmp.right):
curNode = self.right_left_rotation(curNode)
else:
curNode = self.right_right_rotation(curNode)
elif data > curNode.key:
curNode.right = self.deleteoption(data, curNode.right)
if self.getNodeHeight(curNode.left) - self.getNodeHeight(curNode.right) == 2:
tmp = curNode.left
if self.getNodeHeight(tmp.right) > self.getNodeHeight(tmp.left):
curNode = self.left_right_rotation(curNode)
else:
curNode = self.left_left_rotation(curNode)
else:
if curNode.left and curNode.right: # 当前结点是要被删除的结点且当前结点具有左右两棵子树
# 如果curNode的左子树不比右子树高;
# 则(01)找出curNode的右子树中的最小节点
# (02)将该最小节点的值赋值给curNode。
# (03)删除该最小节点。
# 这类似于用"curNode的右子树中最小节点"做"curNode"的替身;
# 采用这种方式的好处是:删除"curNode的右子树中最小节点"之后,AVL树仍然是平衡的。
if curNode.left.height <= curNode.right.height:
minNode = curNode.right.findMin()
curNode.key = minNode.key
curNode.right = self.deleteoption(curNode.key, curNode.right)
else:
# 如果curNode的左子树比右子树高;
# 则(01)找出curNode的左子树中的最大节点
# (02)将该最大节点的值赋值给curNode。
# (03)删除该最大节点。
# 这类似于用"curNode的左子树中最大节点"做"curNode"的替身;
# 采用这种方式的好处是:删除"curNode的左子树中最大节点"之后,AVL树仍然是平衡的。
maxNode = curNode.left.findMax()
curNode.key = maxNode.key
curNode.left = self.deleteoption(curNode.key, curNode.left)
else: # 当前结点是要被删除的结点且当前结点具有一棵子树
if curNode.right:
curNode = curNode.right
else:
curNode = curNode.left
return curNode
1.1.8 完整实现
# 实现AVL树
# -*- coding: utf-8 -*-
class AVLTree(object):
def __init__(self,key):
self.key=key # 该结点的值
self.left=None
self.right=None
self.height=0 # 该结点的高度
# 查找某个值
def find(self,data):
if data == self.key:
return self
elif data < self.key and self.left:
return self.left.find(data)
elif data > self.key and self.right:
return self.right.find(data)
else:
return None
# 返回树中的最小元素与最大元素的结点
def findMin(self):
if self.left:
return self.left.findMin()
else:
return self
def findMax(self):
tree = self
if tree:
while tree.right:
tree = tree.right
return tree
# 计算结点的高度
def getNodeHeight(self, node):
if node is None:
return -1
else:
return node.height
# 左旋操作
def leftrotation(self, k):
newRoot = k.right
k.right = newRoot.left
newRoot.left = k
k.height = max(self.getNodeHeight(k.right), self.getNodeHeight(k.left)) + 1
newRoot.height = max(self.getNodeHeight(newRoot.right), k.height) + 1
return newRoot
# 右旋操作
def rightrotation(self, k):
newRoot = k.left
k.left = newRoot.right
newRoot.right = k
k.height = max(self.getNodeHeight(k.right), self.getNodeHeight(k.left)) + 1
newRoot.height = max(self.getNodeHeight(newRoot.left), k.height) + 1
return newRoot
# LL操作
def left_left_rotation(self, k):
return self.rightrotation(k)
# RR操作
def right_right_rotation(self, k):
return self.leftrotation(k)
# LR操作
def left_right_rotation(self, k):
k.left = self.leftrotation(k.left)
return self.rightrotation(k)
# RL操作
def right_left_rotation(self, k):
k.right = self.rightrotation(k.right)
return self.leftrotation(k)
# 插入结点操作
def insertoption(self, data, curNode):
if curNode is None:
curNode = AVLTree(data)
elif data < curNode.key:
curNode.left = self.insertoption(data, curNode.left)
# 插入节点后,若AVL树失去平衡,则进行相应的调节。
if self.getNodeHeight(curNode.left) - self.getNodeHeight(curNode.right) == 2:
if data < curNode.left.key:
curNode = self.left_left_rotation(curNode)
else:
curNode = self.left_right_rotation(curNode)
elif data > curNode.key:
curNode.right = self.insertoption(data, curNode.right)
# 插入节点后,若AVL树失去平衡,则进行相应的调节。
if self.getNodeHeight(curNode.right) - self.getNodeHeight(curNode.left) == 2:
if data < curNode.right.key:
curNode = self.right_left_rotation(curNode)
else:
curNode = self.right_right_rotation(curNode)
curNode.height = max(self.getNodeHeight(curNode.right), self.getNodeHeight(curNode.left)) + 1
return curNode
# 删除操作
def deleteoption(self, data, curNode):
if curNode is None:
print('AVL树中不存在该值的结点')
raise KeyError
elif data < curNode.key:
curNode.left = self.deleteoption(data, curNode.left)
if self.getNodeHeight(curNode.right) - self.getNodeHeight(curNode.left) == 2:
tmp = curNode.right
if self.getNodeHeight(tmp.left) > self.getNodeHeight(tmp.right):
curNode = self.right_left_rotation(curNode)
else:
curNode = self.right_right_rotation(curNode)
elif data > curNode.key:
curNode.right = self.deleteoption(data, curNode.right)
if self.getNodeHeight(curNode.left) - self.getNodeHeight(curNode.right) == 2:
tmp = curNode.left
if self.getNodeHeight(tmp.right) > self.getNodeHeight(tmp.left):
curNode = self.left_right_rotation(curNode)
else:
curNode = self.left_left_rotation(curNode)
else:
if curNode.left and curNode.right: # 当前结点是要被删除的结点且当前结点具有左右两棵子树
# 如果curNode的左子树不比右子树高;
# 则(01)找出curNode的右子树中的最小节点
# (02)将该最小节点的值赋值给curNode。
# (03)删除该最小节点。
# 这类似于用"curNode的右子树中最小节点"做"curNode"的替身;
# 采用这种方式的好处是:删除"curNode的右子树中最小节点"之后,AVL树仍然是平衡的。
if curNode.left.height <= curNode.right.height:
minNode = curNode.right.findMin()
curNode.key = minNode.key
curNode.right = self.deleteoption(curNode.key, curNode.right)
else:
# 如果curNode的左子树比右子树高;
# 则(01)找出curNode的左子树中的最大节点
# (02)将该最大节点的值赋值给curNode。
# (03)删除该最大节点。
# 这类似于用"curNode的左子树中最大节点"做"curNode"的替身;
# 采用这种方式的好处是:删除"curNode的左子树中最大节点"之后,AVL树仍然是平衡的。
maxNode = curNode.left.findMax()
curNode.key = maxNode.key
curNode.left = self.deleteoption(curNode.key, curNode.left)
else: # 当前结点是要被删除的结点且当前结点具有一棵子树
if curNode.right:
curNode = curNode.right
else:
curNode = curNode.left
return curNode
# 中序遍历,使用递归,返回list
def inorder(self, nodelist = None):
if nodelist is None:
nodelist = []
if self:
if self.left:
self.left.inorder(nodelist)
nodelist.append(self.key)
if self.right:
self.right.inorder(nodelist)
return nodelist
def preorder(self, nodelist = None):
if nodelist is None:
nodelist = []
if self:
nodelist.append(self.key)
if self.left:
self.left.preorder(nodelist)
if self.right:
self.right.preorder(nodelist)
return nodelist
def postorder(self, nodelist = None):
if nodelist is None:
nodelist = []
if self:
if self.left:
self.left.postorder(nodelist)
if self.right:
self.right.postorder(nodelist)
nodelist.append(self.key)
return nodelist
if __name__ == '__main__':
mlist = [3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9]
print(mlist)
print("初始化AVL树...")
tree = AVLTree(mlist[0])
print('依次插入...')
for i in mlist[1:]:
tree = tree.insertoption(i, tree)
print("中序遍历: ")
print(tree.inorder())
print("先序遍历: ")
print(tree.preorder())
print("后序遍历: ")
print(tree.postorder())
print('最大值:',tree.findMax().key)
print('最小值:',tree.findMin().key)
print('删除结点值为8的结点')
tree = tree.deleteoption(8, tree)
print("中序遍历: ")
print(tree.inorder())
print("先序遍历: ")
print(tree.preorder())
print("后序遍历: ")
print(tree.postorder())
print('查找值为9的结点', tree.find(9).key)
输出:
[3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9]
初始化AVL树...
依次插入...
中序遍历:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
先序遍历:
[7, 4, 2, 1, 3, 6, 5, 13, 11, 9, 8, 10, 12, 15, 14, 16]
后序遍历:
[1, 3, 2, 5, 6, 4, 8, 10, 9, 12, 11, 14, 16, 15, 13, 7]
最大值: 16
最小值: 1
删除结点值为8的结点
中序遍历:
[1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16]
先序遍历:
[7, 4, 2, 1, 3, 6, 5, 13, 11, 9, 10, 12, 15, 14, 16]
后序遍历:
[1, 3, 2, 5, 6, 4, 10, 9, 12, 11, 14, 16, 15, 13, 7]
查找值为9的结点 9
2 红黑树
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,典型的用途是实现关联数组(又称映射、字典)。红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树。
红黑树满足二叉查找树的特征:任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。除了具备该特性之外,红黑树每个节点上都有存储位表示节点的颜色,颜色是红(Red)或黑(Black)。
红黑树的特性:
- 每个节点是黑色或红色。
- 根节点是黑色。
- 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从一个节点到该节点的每个叶子节点的所有路径上包含相同数目的黑色节点。

红黑树的应用: 红黑树主要是被用来存储有序的数据,它的时间复杂度是$O(\log n)$,效率非常之高。例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
黑高度: 从某个节点$x$出发(不包括该节点)到达一个叶节点的任意一条路径上,黑色节点的个数称为该节点的黑高度(x’s black height),记为$bh(x)$。从节点$x$出发达到叶节点”所经历的黑节点数目”>= “所经历的红节点的数目”。
定理1: 一棵含有$n$个节点的红黑树的高度至多为$2\log_2(n+1)$。
定理2: 高度为$h$的红黑树,它的包含的黑节点个数至少为$2bh(x)-1$个。
2.1 代码实现
2.1.1 红黑树定义
class Node(object):
def __init__(self, key):
self.key = key
self.color = 'black'
self.left = None
self.right = None
self.parent = None
class RedBlackTree(object):
def __init__(self):
self.root = None
2.1.2 查找
# 查找操作
def find(self, node, data):
if data == node.key:
return node
elif data < node.key and node.left:
return self.find(node.left, data)
elif data > node.key and node.right:
return self.find(node.right, data)
else:
return None
2.1.3 获取最大值最小值
# 返回树中的最小元素与最大元素的结点
def findMin(self, node):
if node.left:
return self.findMin(node.left)
else:
return node
def findMax(self, node):
tree = node
if tree:
while tree.right:
tree = tree.right
return tree
2.1.4 前驱结点
# 找结点(node)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。
def predecessor(self, node):
# 如果node存在左孩子,则"node的前驱结点"为"以其左孩子为根的子树的最大结点"
if node.left:
return self.findMax(node.left)
# 如果node没有左孩子。则node有以下两种可能:
# (1) node"一个右孩子",则"node的前驱结点"为 "它的父结点"
# (2) node是"一个左孩子",则查找"node的最低的父结点,并且该父结点要具有右孩子",
# 找到的这个"最低的父结点"就是"node的前驱结点"
preNode = node.parent
while preNode and node == preNode.left:
node = preNode
preNode = preNode.parent
return preNode
2.1.5 后继结点
# 找结点(node)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。
def successor(self, node):
# 如果node存在右孩子,则"node的后继结点"为 "以其右孩子为根的子树的最小结点"
if node.right:
return self.findMin(node.right)
# 如果node没有右孩子。则node有以下两种可能:
# (1) node是"一个左孩子",则"node的后继结点"为"它的父结点"
# (2) node是"一个右孩子",则查找"node的最低的父结点,并且该父结点要具有左孩子",
# 找到的这个"最低的父结点"就是"node的后继结点"
sucNode = node.parent
while sucNode and node == sucNode.right:
node = sucNode
sucNode = sucNode.parent
return sucNode
2.1.6 左旋操作
# 左旋
def leftrotation(self, k):
# 以K为根节点的子树中设置K的右孩子为新的根节点newRoot
newRoot = k.right
# 将 “newRoot的左孩子” 设为 “k的右孩子”;
k.right = newRoot.left
# 如果"newRoot的左孩子"不为空的话,将 “k” 设为 “newRoot的左孩子的父亲”
if newRoot.left:
newRoot.left.parent = k
# 将 “k的父亲” 设为 “newRoot的父亲”
newRoot.parent = k.parent
if k.parent is None:
# 如果 “k的父亲” 是空节点,则将newRoot设为根节点
self.root = newRoot
else:
if k.parent.left == k:
# 如果 k是它父节点的左孩子,则将newRoot设为“k的父节点的左孩子”
k.parent.left = newRoot
else:
k.parent.right = newRoot
# 将 “k” 设为 “newRoot的左孩子”
newRoot.left = k
# 将 “k的父节点” 设为 “newRoot”
k.parent = newRoot
2.1.7 右旋操作
# 右旋
def rightrotation(self, k):
# 以K为根节点的子树中设置K的左孩子为新的根节点newRoot
newRoot = k.left
# 将 “newRoot的右孩子” 设为 “k的左孩子”;
k.left = newRoot.right
# 如果"newRoot的右孩子"不为空的话,将 “k” 设为 “newRoot的右孩子的父亲”
if newRoot.right:
newRoot.right.parent = k
# 将 “k的父亲” 设为 “newRoot的父亲”
newRoot.parent = k.parent
if k.parent is None:
# 如果 “k的父亲” 是空节点,则将newRoot设为根节点
self.root = newRoot
else:
if k.parent.left == k:
# 如果 k是它父节点的左孩子,则将newRoot设为“k的父节点的左孩子”
k.parent.left = newRoot
else:
k.parent.right = newRoot
# 将 “k” 设为 “newRoot的右孩子”
newRoot.right = k
# 将 “k的父节点” 设为 “newRoot”
k.parent = newRoot
2.1.8 插入操作
分三步:
- 将红黑树当作一颗二叉查找树,将节点插入。
- 将插入的节点着色为”红色”。
- 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
# 插入操作
def insertoption(self, data):
insertnode = Node(data)
if self.root is None:
self.root = insertnode
elif not self.find(self.root, data):
self.insert(insertnode)
# 插入结点
def insert(self, node):
curNode = self.root
# 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中
while curNode:
tmp = curNode
if node.key < curNode.key:
curNode = curNode.left
else:
curNode = curNode.right
node.parent = tmp
if tmp:
if node.key < tmp.key:
tmp.left = node
else:
tmp.right = node
else:
self.root = node
# 设置节点的颜色为红色
node.color = 'red'
# 将它重新修正为一颗红黑树
self.insertfix(node)
# 修正插入后的红黑树
# 在向红黑树中插入节点之后(失去平衡),再调用该函数;
# 目的是将它重新塑造成一颗红黑树。
def insertfix(self, node):
# 若“父节点存在,并且父节点的颜色是红色”
while node.parent and node.parent.color == 'red':
# parentNode = node.parent
# grandparentNode = parentNode.parent
# 若“父节点”是“祖父节点的左孩子”
if node.parent == node.parent.parent.left:
uncleNode = node.parent.parent.right
# Case 1条件:叔叔节点是红色
if uncleNode and uncleNode.color == 'red':
uncleNode.color = 'black'
node.parent.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
# Case 2条件:叔叔是黑色,且当前节点是右孩子
if node == node.parent.right:
node = node.parent
self.leftrotation(node)
# Case 3条件:叔叔是黑色,且当前节点是左孩子。
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.rightrotation(node.parent.parent)
else:
# 若“父节点”是“祖父节点的右孩子”
uncleNode = node.parent.parent.left
# Case 1条件:叔叔节点是红色
if uncleNode and uncleNode.color == 'red':
uncleNode.color = 'black'
node.parent.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
# Case 2条件:叔叔是黑色,且当前节点是左孩子
if node == node.parent.left:
node = node.parent
self.rightrotation(node)
# Case 3条件:叔叔是黑色,且当前节点是右孩子。
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.leftrotation(node.parent.parent)
self.root.color = 'black'
2.1.9 删除操作
分三种情况:
- 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
- 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
- 被删除节点有两个儿子。
- 先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;
- 之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给”被删除节点”之后,再将后继节点删除。这样就巧妙的将问题转换为”删除后继节点”的情况了,下面就考虑后继节点。在”被删除节点”有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然”的后继节点”不可能双子都非空,就意味着”该节点的后继节点”要么没有儿子,要么只有一个儿子。若没有儿子,则按”情况1”进行处理;若只有一个儿子,则按”情况2 “进行处理。
删除结点之后,可能会违背红黑树的特性,需要对红黑树进行修正。
# 删除操作
def deleteoption(self, data):
deleteNode = self.find(self.root, data)
if deleteNode:
self.delete(deleteNode)
# 删除结点
def delete(self, node):
# 被删除节点的"左右孩子都不为空"的情况
if node.left and node.right:
# 找到被删节点的后继节点(称为"取代节点"),用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
replaceNode = self.successor(node)
# "node节点"不是根节点(只有根节点不存在父节点)
if node.parent:
if node.parent.left == node:
node.parent.left = replaceNode
else:
node.parent.right = replaceNode
else:
# "node节点"是根节点,更新根节点。
self.root = replaceNode
# childNode是"取代节点"的右孩子,也是需要"调整的节点"。
# "取代节点"肯定不存在左孩子!因为它是一个后继节点。
childNode = replaceNode.right
parentNode = replaceNode.parent
# 保存"取代节点"的颜色
color = replaceNode.color
# "被删除节点"是"它的后继节点的父节点"
if parentNode == node:
parentNode = replaceNode
else:
# childNode不为空
if childNode:
childNode.parent = parentNode
parentNode.left = childNode
replaceNode.right = node.right
node.right.parent = replaceNode
replaceNode.parent = node.parent
replaceNode.color = node.color
replaceNode.left = node.left
node.left.parent = replaceNode
if color == 'black':
self.deletefix(childNode, parentNode)
node = None
return
if node.left:
childNode = node.left
else:
childNode = node.right
parentNode = node.parent
# 保存"取代节点"的颜色
color = node.color
if childNode:
childNode.parent = parentNode
# "node节点"不是根节点
if parentNode:
if parentNode.left == node:
parentNode.left = childNode
else:
parentNode.right = childNode
else:
self.root = childNode
if color == 'black':
self.deletefix(childNode, parentNode)
node = None
# 修正删除后的红黑树
# 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
# 目的是将它重新塑造成一颗红黑树。
# childNode:待修正的结点
def deletefix(self, node, parentNode):
while node.color == 'black' and node != self.root:
if parentNode.left == node:
tmp = parentNode.right
if tmp.color == 'red':
# Case 1: node的兄弟tmp是红色的
tmp.color = 'black'
parentNode.color = 'red'
self.leftrotation(parentNode)
tmp = parentNode.right
else:
if tmp.left.color == 'black' and tmp.right.color == 'black':
# Case 2: node的兄弟tmp是黑色,且tmp的俩个孩子也都是黑色的
tmp.color = 'red'
node = parentNode
parentNode = node.parent
else:
if tmp.right.color == 'black':
# Case 3: node的兄弟tmp是黑色的,并且tmp的左孩子是红色,右孩子为黑色。
tmp.left.color = 'black'
tmp.color = 'red'
self.rightrotation(tmp)
tmp = parentNode.right
else:
# Case 4: node的兄弟tmp是黑色的;并且tmp的右孩子是红色的,左孩子黑色。
tmp.color = parentNode.color
parentNode.color = 'black'
tmp.right.color = 'black'
self.leftrotation(parentNode)
node = self.root
break
else:
# node是parentNode的右结点
tmp = parentNode.right
if tmp.color == 'red':
# Case 1: node的兄弟tmp是红色的
tmp.color = 'black'
parentNode.color = 'red'
self.rightrotation(parentNode)
tmp = parentNode.left
else:
if tmp.left.color == 'black' and tmp.right.color == 'black':
# Case 2: node的兄弟tmp是黑色,且tmp的俩个孩子也都是黑色的
tmp.color = 'red'
node = parentNode
parentNode = node.parent
else:
if tmp.left.color == 'black':
# Case 3: node的兄弟tmp是黑色的,并且tmp的右孩子是红色,左孩子为黑色。
tmp.right.color = 'black'
tmp.color = 'red'
self.leftrotation(tmp)
tmp = parentNode.left
else:
# Case 4: node的兄弟tmp是黑色的;并且tmp的左孩子是红色的,右孩子黑色。
tmp.color = parentNode.color
parentNode.color = 'black'
tmp.left.color = 'black'
self.rightrotation(parentNode)
node = self.root
break
if node:
node.color = 'black'
2.1.10 完整实现
# 实现红黑树
# -*- coding: utf-8 -*-
class Node(object):
def __init__(self, key):
self.key = key
self.color = 'black'
self.left = None
self.right = None
self.parent = None
class RedBlackTree(object):
def __init__(self):
self.root = None
# 查找操作
def find(self, node, data):
if data == node.key:
return node
elif data < node.key and node.left:
return self.find(node.left, data)
elif data > node.key and node.right:
return self.find(node.right, data)
else:
return None
# 返回树中的最小元素与最大元素的结点
def findMin(self, node):
if node.left:
return self.findMin(node.left)
else:
return node
def findMax(self, node):
tree = node
if tree:
while tree.right:
tree = tree.right
return tree
# 找结点(node)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。
def predecessor(self, node):
# 如果node存在左孩子,则"node的前驱结点"为"以其左孩子为根的子树的最大结点"
if node.left:
return self.findMax(node.left)
# 如果node没有左孩子。则node有以下两种可能:
# (1) node"一个右孩子",则"node的前驱结点"为 "它的父结点"
# (2) node是"一个左孩子",则查找"node的最低的父结点,并且该父结点要具有右孩子",
# 找到的这个"最低的父结点"就是"node的前驱结点"
preNode = node.parent
while preNode and node == preNode.left:
node = preNode
preNode = preNode.parent
return preNode
# 找结点(node)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。
def successor(self, node):
# 如果node存在右孩子,则"node的后继结点"为 "以其右孩子为根的子树的最小结点"
if node.right:
return self.findMin(node.right)
# 如果node没有右孩子。则node有以下两种可能:
# (1) node是"一个左孩子",则"node的后继结点"为"它的父结点"
# (2) node是"一个右孩子",则查找"node的最低的父结点,并且该父结点要具有左孩子",
# 找到的这个"最低的父结点"就是"node的后继结点"
sucNode = node.parent
while sucNode and node == sucNode.right:
node = sucNode
sucNode = sucNode.parent
return sucNode
# 左旋
def leftrotation(self, k):
# 以K为根节点的子树中设置K的右孩子为新的根节点newRoot
newRoot = k.right
# 将 “newRoot的左孩子” 设为 “k的右孩子”;
k.right = newRoot.left
# 如果"newRoot的左孩子"不为空的话,将 “k” 设为 “newRoot的左孩子的父亲”
if newRoot.left:
newRoot.left.parent = k
# 将 “k的父亲” 设为 “newRoot的父亲”
newRoot.parent = k.parent
if k.parent is None:
# 如果 “k的父亲” 是空节点,则将newRoot设为根节点
self.root = newRoot
else:
if k.parent.left == k:
# 如果 k是它父节点的左孩子,则将newRoot设为“k的父节点的左孩子”
k.parent.left = newRoot
else:
k.parent.right = newRoot
# 将 “k” 设为 “newRoot的左孩子”
newRoot.left = k
# 将 “k的父节点” 设为 “newRoot”
k.parent = newRoot
# 右旋
def rightrotation(self, k):
# 以K为根节点的子树中设置K的左孩子为新的根节点newRoot
newRoot = k.left
# 将 “newRoot的右孩子” 设为 “k的左孩子”;
k.left = newRoot.right
# 如果"newRoot的右孩子"不为空的话,将 “k” 设为 “newRoot的右孩子的父亲”
if newRoot.right:
newRoot.right.parent = k
# 将 “k的父亲” 设为 “newRoot的父亲”
newRoot.parent = k.parent
if k.parent is None:
# 如果 “k的父亲” 是空节点,则将newRoot设为根节点
self.root = newRoot
else:
if k.parent.left == k:
# 如果 k是它父节点的左孩子,则将newRoot设为“k的父节点的左孩子”
k.parent.left = newRoot
else:
k.parent.right = newRoot
# 将 “k” 设为 “newRoot的右孩子”
newRoot.right = k
# 将 “k的父节点” 设为 “newRoot”
k.parent = newRoot
# 插入操作
def insertoption(self, data):
insertnode = Node(data)
if self.root is None:
self.root = insertnode
elif not self.find(self.root, data):
self.insert(insertnode)
# 插入结点
def insert(self, node):
curNode = self.root
# 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中
while curNode:
tmp = curNode
if node.key < curNode.key:
curNode = curNode.left
else:
curNode = curNode.right
node.parent = tmp
if tmp:
if node.key < tmp.key:
tmp.left = node
else:
tmp.right = node
else:
self.root = node
# 设置节点的颜色为红色
node.color = 'red'
# 将它重新修正为一颗红黑树
self.insertfix(node)
# 修正插入后的红黑树
# 在向红黑树中插入节点之后(失去平衡),再调用该函数;
# 目的是将它重新塑造成一颗红黑树。
def insertfix(self, node):
# 若“父节点存在,并且父节点的颜色是红色”
while node.parent and node.parent.color == 'red':
# parentNode = node.parent
# grandparentNode = parentNode.parent
# 若“父节点”是“祖父节点的左孩子”
if node.parent == node.parent.parent.left:
uncleNode = node.parent.parent.right
# Case 1条件:叔叔节点是红色
if uncleNode and uncleNode.color == 'red':
uncleNode.color = 'black'
node.parent.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
# Case 2条件:叔叔是黑色,且当前节点是右孩子
if node == node.parent.right:
node = node.parent
self.leftrotation(node)
# Case 3条件:叔叔是黑色,且当前节点是左孩子。
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.rightrotation(node.parent.parent)
else:
# 若“父节点”是“祖父节点的右孩子”
uncleNode = node.parent.parent.left
# Case 1条件:叔叔节点是红色
if uncleNode and uncleNode.color == 'red':
uncleNode.color = 'black'
node.parent.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
# Case 2条件:叔叔是黑色,且当前节点是左孩子
if node == node.parent.left:
node = node.parent
self.rightrotation(node)
# Case 3条件:叔叔是黑色,且当前节点是右孩子。
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.leftrotation(node.parent.parent)
self.root.color = 'black'
# 删除操作
def deleteoption(self, data):
deleteNode = self.find(self.root, data)
if deleteNode:
self.delete(deleteNode)
# 删除结点
def delete(self, node):
# 被删除节点的"左右孩子都不为空"的情况
if node.left and node.right:
# 找到被删节点的后继节点(称为"取代节点"),用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
replaceNode = self.successor(node)
# "node节点"不是根节点(只有根节点不存在父节点)
if node.parent:
if node.parent.left == node:
node.parent.left = replaceNode
else:
node.parent.right = replaceNode
else:
# "node节点"是根节点,更新根节点。
self.root = replaceNode
# childNode是"取代节点"的右孩子,也是需要"调整的节点"。
# "取代节点"肯定不存在左孩子!因为它是一个后继节点。
childNode = replaceNode.right
parentNode = replaceNode.parent
# 保存"取代节点"的颜色
color = replaceNode.color
# "被删除节点"是"它的后继节点的父节点"
if parentNode == node:
parentNode = replaceNode
else:
# childNode不为空
if childNode:
childNode.parent = parentNode
parentNode.left = childNode
replaceNode.right = node.right
node.right.parent = replaceNode
replaceNode.parent = node.parent
replaceNode.color = node.color
replaceNode.left = node.left
node.left.parent = replaceNode
if color == 'black':
self.deletefix(childNode, parentNode)
node = None
return
if node.left:
childNode = node.left
else:
childNode = node.right
parentNode = node.parent
# 保存"取代节点"的颜色
color = node.color
if childNode:
childNode.parent = parentNode
# "node节点"不是根节点
if parentNode:
if parentNode.left == node:
parentNode.left = childNode
else:
parentNode.right = childNode
else:
self.root = childNode
if color == 'black':
self.deletefix(childNode, parentNode)
node = None
# 修正删除后的红黑树
# 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
# 目的是将它重新塑造成一颗红黑树。
# childNode:待修正的结点
def deletefix(self, node, parentNode):
while node.color == 'black' and node != self.root:
if parentNode.left == node:
tmp = parentNode.right
if tmp.color == 'red':
# Case 1: node的兄弟tmp是红色的
tmp.color = 'black'
parentNode.color = 'red'
self.leftrotation(parentNode)
tmp = parentNode.right
else:
if tmp.left.color == 'black' and tmp.right.color == 'black':
# Case 2: node的兄弟tmp是黑色,且tmp的俩个孩子也都是黑色的
tmp.color = 'red'
node = parentNode
parentNode = node.parent
else:
if tmp.right.color == 'black':
# Case 3: node的兄弟tmp是黑色的,并且tmp的左孩子是红色,右孩子为黑色。
tmp.left.color = 'black'
tmp.color = 'red'
self.rightrotation(tmp)
tmp = parentNode.right
else:
# Case 4: node的兄弟tmp是黑色的;并且tmp的右孩子是红色的,左孩子黑色。
tmp.color = parentNode.color
parentNode.color = 'black'
tmp.right.color = 'black'
self.leftrotation(parentNode)
node = self.root
break
else:
# node是parentNode的右结点
tmp = parentNode.right
if tmp.color == 'red':
# Case 1: node的兄弟tmp是红色的
tmp.color = 'black'
parentNode.color = 'red'
self.rightrotation(parentNode)
tmp = parentNode.left
else:
if tmp.left.color == 'black' and tmp.right.color == 'black':
# Case 2: node的兄弟tmp是黑色,且tmp的俩个孩子也都是黑色的
tmp.color = 'red'
node = parentNode
parentNode = node.parent
else:
if tmp.left.color == 'black':
# Case 3: node的兄弟tmp是黑色的,并且tmp的右孩子是红色,左孩子为黑色。
tmp.right.color = 'black'
tmp.color = 'red'
self.leftrotation(tmp)
tmp = parentNode.left
else:
# Case 4: node的兄弟tmp是黑色的;并且tmp的左孩子是红色的,右孩子黑色。
tmp.color = parentNode.color
parentNode.color = 'black'
tmp.left.color = 'black'
self.rightrotation(parentNode)
node = self.root
break
if node:
node.color = 'black'
# 中序遍历,使用递归,返回list
def inorder(self, node, nodelist = None):
if nodelist is None:
nodelist = []
if node:
if node.left:
self.inorder(node.left, nodelist)
nodelist.append(node.key)
if node.right:
self.inorder(node.right, nodelist)
return nodelist
def preorder(self, node, nodelist = None):
if nodelist is None:
nodelist = []
if node:
nodelist.append(node.key)
if node.left:
self.preorder(node.left, nodelist)
if node.right:
self.preorder(node.right, nodelist)
return nodelist
def postorder(self, node, nodelist = None):
if nodelist is None:
nodelist = []
if node:
if node.left:
self.postorder(node.left, nodelist)
if node.right:
self.postorder(node.right, nodelist)
nodelist.append(node.key)
return nodelist
def mprint(self, node, data, direction):
if node:
if direction == 0:
print('%2d(%s) is root' % (node.key, node.color))
else:
tmp = "right" if direction == 1 else "left"
print("%2d(%s) is %2d's %6s child" % (node.key, node.color, data, tmp))
self.mprint(node.left, node.key, -1)
self.mprint(node.right, node.key, 1)
if __name__ == '__main__':
mlist = [10, 40, 30, 60, 90, 70, 20, 50, 80]
print('原始数据:', mlist)
print("初始化红黑树...")
tree = RedBlackTree()
print('依次插入...')
for i in mlist:
tree.insertoption(i)
print("中序遍历: ")
print(tree.inorder(tree.root))
print("先序遍历: ")
print(tree.preorder(tree.root))
print("后序遍历: ")
print(tree.postorder(tree.root))
tree.mprint(tree.root, tree.root.key, 0)
print('最大值:', tree.findMax(tree.root).key)
print('最小值:', tree.findMin(tree.root).key)
print('删除值为30的结点')
tree.deleteoption(30)
tree.mprint(tree.root, tree.root.key, 0)
输出:
原始数据: [10, 40, 30, 60, 90, 70, 20, 50, 80]
初始化红黑树...
依次插入...
中序遍历:
[10, 20, 30, 40, 50, 60, 70, 80, 90]
先序遍历:
[30, 10, 20, 60, 40, 50, 80, 70, 90]
后序遍历:
[20, 10, 50, 40, 70, 90, 80, 60, 30]
30(black) is root
10(black) is 30's left child
20(red) is 10's right child
60(red) is 30's right child
40(black) is 60's left child
50(red) is 40's right child
80(black) is 60's right child
70(red) is 80's left child
90(red) is 80's right child
最大值: 90
最小值: 10
删除值为30的结点
40(black) is root
10(black) is 40's left child
20(red) is 10's right child
60(red) is 40's right child
50(black) is 60's left child
80(black) is 60's right child
70(red) is 80's left child
90(red) is 80's right child
3 总结
二叉查找树:
- 查找最好时间复杂度
$O(\log_2N)$,最坏时间复杂度$O(N)$。 - 插入删除操作算法简单,时间复杂度与查找差不多
AVL树:
- 查找的时间复杂度维持在
$O(\log_2N)$,不会出现最差情况 - AVL树在执行每个插入操作时最多需要1次旋转,其时间复杂在
$O(\log_2N)$左右。 - AVL树在执行删除时代价稍大,执行每个删除操作的时间复杂度需要
$O(2\log_2N)$。
红黑树:
- 查找效率最好情况下时间复杂度为
$O(\log_2N)$,但在最坏情况下比AVL要差一些,但也远远好于二叉查找树。 - 插入和删除操作改变树的平衡性的概率要远远小于AVL(红黑树不是高度平衡的)。因此需要的旋转操作的可能性要小,而且一旦需要旋转,插入一个结点最多只需要旋转2次,删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在
$O(\log_2N)$,但是实际上,这种操作由于简单所需要的代价很小。
注意: 红黑树适用于插入删除频繁,AVL树适用于查找频繁。
参考文献
平衡二叉搜索树-维基百科
AVL树(一)之 图文解析和C语言的实现
AVL树的python实现
红黑树(一)之 原理和算法详细介绍
