数据结构——堆结构
1 堆结构
堆(英语:Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。
堆也被称为优先队列(priority queue),队列中允许的操作是先进先出(FIFO),在队尾插入元素,在队头取出元素。而堆也是一样,在堆底插入元素,在堆顶取出元素,但是堆中元素的排列不是按照到来的先后顺序,而是按照一定的优先顺序排列的。这个优先顺序可以是元素的大小或者其他规则。如图一所示就是一个堆,堆优先顺序就是大的元素排在前面,小的元素排在后面,这样得到的堆称为最大堆。最大堆中堆顶的元素是整个堆中最大的,并且每一个分支也可以看成一个最大堆。同样的,我们可以定义最小堆,如图二所示。
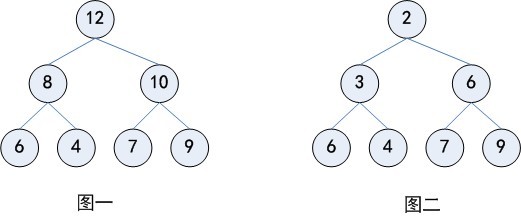
堆通常也可以被看做一棵树,它满足下列性质:
- 堆中任意节点的值总是不大于(不小于)其子节点的值;
- 堆总是一棵完全树,即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
将任意节点不大于其子节点的堆叫做最小堆或小根堆,而将任意节点不小于其子节点的堆叫做最大堆或大根堆。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。
2 二叉堆
二叉堆是一种特殊的堆,二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性:父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
- 当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。
- 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
二叉堆一般都通过”数组“来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将”二叉堆的第一个元素”放在数组索引0的位置,有时候放在索引1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。
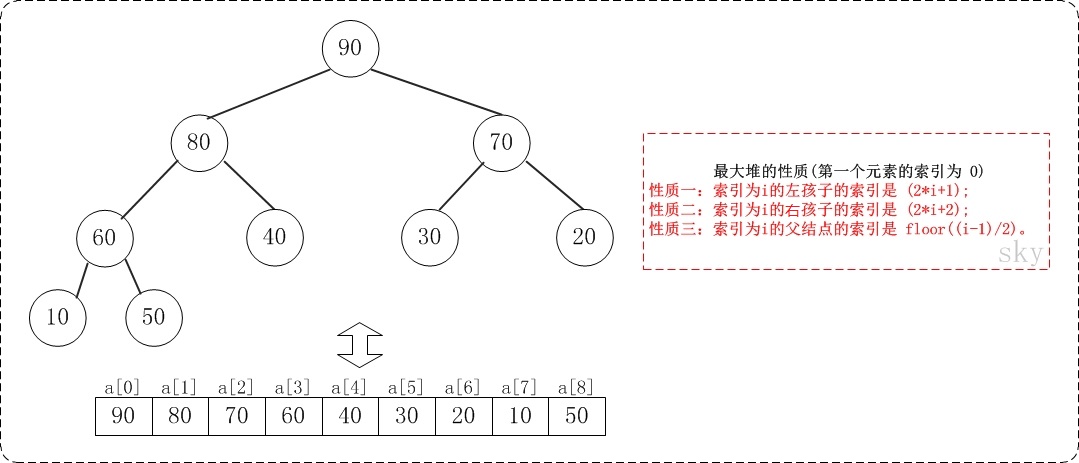
假设”第一个元素”在数组中的索引为0 的话,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引是 (2*i+1);
- 索引为i的右孩子的索引是 (2*i+2);
- 索引为i的父结点的索引是 floor((i-1)/2);
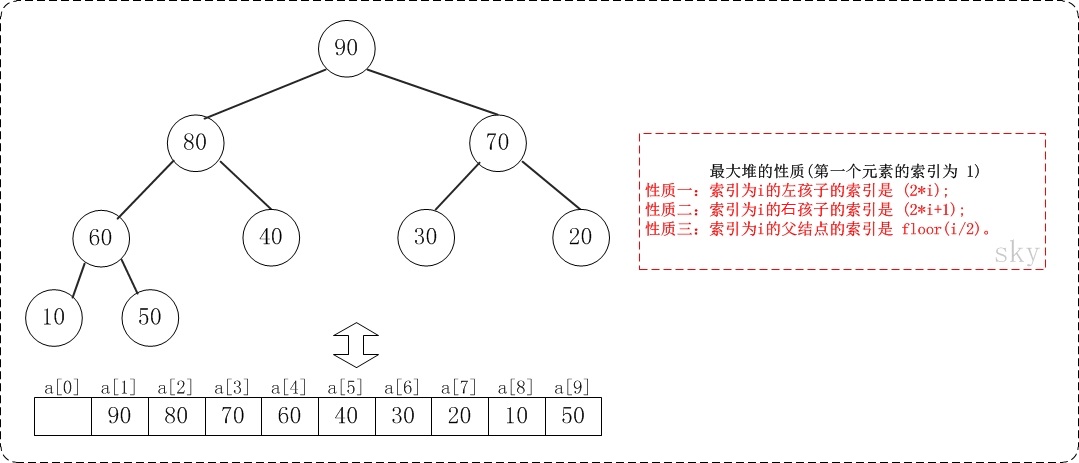
假设”第一个元素”在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引是 (2*i);
- 索引为i的右孩子的索引是 (2*i+1);
- 索引为i的父结点的索引是 floor(i/2);
2.1 基本操作
接下来使用最小堆来进行操作,基本操作定义如下:
MinBinaryHeap():创建一个空的二叉堆对象min_insert(self,data):将新元素加入到堆中remove(self,data):删除堆中某个元素minChild(self, i):返回子树中最小的索引值buildHeap(list):从一个包含节点的列表里创建新堆
2.2 操作的实现
2.2.1 二叉堆结构
接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据,构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。
class MinBinaryHeap(object):
def __init__(self):
self.heaplist = []
self.currentsize = 0
2.2.2 插入
当从最小堆中插入数据时:首先,为了满足“完全二叉树”的性质,新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾,显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小,可以与父节点互换位置。直到形成一个最小堆。如下图所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。
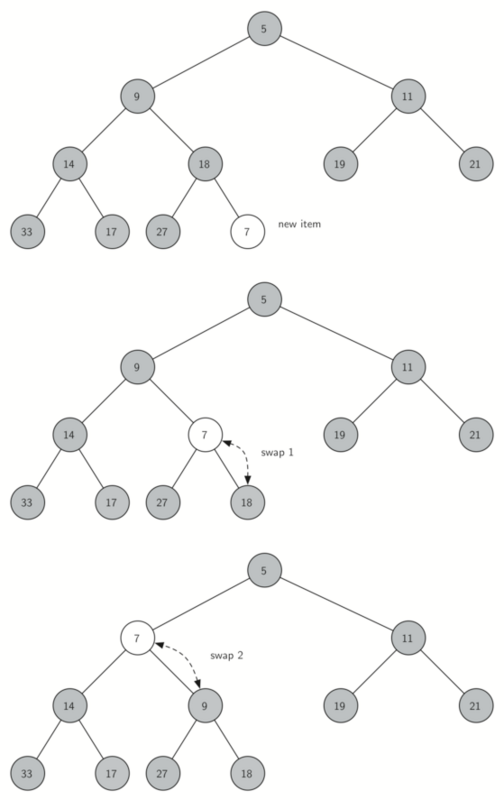
# “上浮”方法,它把一个新节点“上浮”到其正确位置来满足堆次序。
def min_percUp(self, n):
# 一直循环到根节点,也就是数组中索引为0的数值,当索引小于0则不在数组中跳出循环
while ((n - 1) // 2) >= 0:
# 比较这个节点和父节点的大小
if self.heaplist[n] < self.heaplist[(n - 1) // 2]:
temp = self.heaplist[(n - 1) // 2]
self.heaplist[(n - 1) // 2] = self.heaplist[n]
self.heaplist[n] = temp
n = (n - 1) // 2 # 将指针移到该节点的父节点,然后继续上浮
def min_insert(self, data):
self.heaplist.append(data)
self.currentsize += 1
self.min_percUp(self.currentsize - 1)
2.2.3 删除
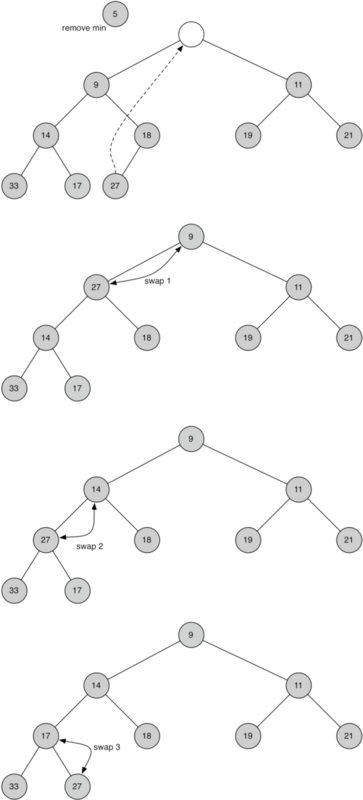
当从最小堆中删除数据时:先删除该数据,然后用最小堆中最后一个的元素插入这个空位;接着,为了保持堆次序,我们需将这个“空位”沿着一条路径“下沉”,直到比两个子节点都小。在选择下沉路径时,如果这个“空位”比子节点大,那么选择较小的子节点与之交换。如下图所示的是删除一个元素后“下沉”操作的过程。
# 删除某个节点的数据
def min_delete(self, data):
index = self.heaplist.index(data) # 先确定删除节点的索引
if index == self.currentsize - 1: # 当删除节点在列表末尾直接删除
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
else:
self.heaplist[index] = self.heaplist[-1] # 将列表末尾数放到删除节点的位置
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
self.min_percDown(index)
# 返回子树中最小的索引值
def minChild(self, i):
# 如果该节点没有右孩子,那么左孩子就是最小值
if i * 2 + 2 > self.currentsize - 1:
return i * 2 + 1
else:
# 如果存在左右孩子,返回最小的那个
if self.heaplist[i * 2 + 1] < self.heaplist[i * 2 + 2]:
return i * 2 + 1
else:
return i * 2 + 2
# “下沉”操作
def min_percDown(self, n):
# 如果这个节点有左孩子,则进入循环
while n * 2 + 1 <= self.currentsize - 1:
mc = self.minChild(n) # 确定该节点的最小的孩子的索引值
# 如果该节点值大于孩子节点最小的值,则进行交换
if self.heaplist[n] > self.heaplist[mc]:
temp = self.heaplist[mc]
self.heaplist[mc] = self.heaplist[n]
self.heaplist[n] = temp
n = mc # 更新当前节点的位置,继续下沉
2.2.4 生成最小堆
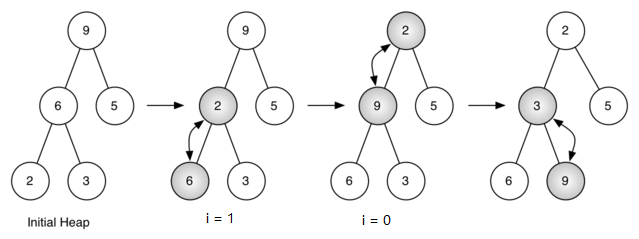
上图所示的是利用buildminHeap方法将最开始的树$[9,6,5,2,3]$中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始,然后回溯到根节点,但min_percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树,任何在中间的节点都是叶节点,因此没有子节点。注意,当$i=0$时,我们从根节点开始下沉,这就需要进行大量的交换操作。可以看到,上图最右边的两颗树,首先$9$从根节点的位置移走,移到下一层级之后,min_percDown进一步检查它此时的子节点,保证它下降到不能再下降为止,即下降到正确的位置。然后进行第二次交换,$9$和$3$的交换。由于$9$已经移到了树最底层的层级,便无法进一步交换了。
def buildminHeap(self, data):
i = len(data) // 2 - 1
self.currentsize = len(data)
self.heaplist = data
while i >= 0:
self.min_percDown(i)
i = i - 1
2.2.5 最小堆的完整实现
class MinBinaryHeap(object):
def __init__(self):
self.heaplist = []
self.currentsize = 0
# “上浮”方法,它把一个新节点“上浮”到其正确位置来满足堆次序。
def min_percUp(self, n):
# 一直循环到根节点,也就是数组中索引为 0的数值,当索引小于 0则不在数组中跳出循环
while ((n - 1) // 2) >= 0:
# 比较这个节点和父节点的大小
if self.heaplist[n] < self.heaplist[(n - 1) // 2]:
temp = self.heaplist[(n - 1) // 2]
self.heaplist[(n - 1) // 2] = self.heaplist[n]
self.heaplist[n] = temp
n = (n - 1) // 2 # 将指针移到该节点的父节点,然后继续上浮
def min_insert(self, data):
self.heaplist.append(data)
self.currentsize += 1
self.min_percUp(self.currentsize - 1)
# 删除某个节点的数据
def min_delete(self, data):
index = self.heaplist.index(data) # 先确定删除节点的索引
if index == self.currentsize - 1: # 当删除节点在列表末尾直接删除
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
else:
self.heaplist[index] = self.heaplist[-1] # 将列表末尾数放到删除节点的位置
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
self.min_percDown(index)
# 返回子树中最小的索引值
def minChild(self, i):
# 如果该节点没有右孩子,那么左孩子就是最小值
if i * 2 + 2 > self.currentsize - 1:
return i * 2 + 1
else:
# 如果存在左右孩子,返回最小的那个
if self.heaplist[i * 2 + 1] < self.heaplist[i * 2 + 2]:
return i * 2 + 1
else:
return i * 2 + 2
# “下沉”操作
def min_percDown(self, n):
# 如果这个节点有左孩子,则进入循环
while n * 2 + 1 <= self.currentsize - 1:
mc = self.minChild(n) # 确定该节点的最小的孩子的索引值
# 如果该节点值大于孩子节点最小的值,则进行交换
if self.heaplist[n] > self.heaplist[mc]:
temp = self.heaplist[mc]
self.heaplist[mc] = self.heaplist[n]
self.heaplist[n] = temp
n = mc # 更新当前节点的位置,继续下沉
def buildminHeap(self, data):
i = len(data) // 2 - 1
self.currentsize = len(data)
self.heaplist = data
while i >= 0:
self.min_percDown(i)
i = i - 1
2.2.6 最大堆的完整实现
最大堆的实现和最小堆类似,这里就不在赘述了。下面直接提供最大堆的实现。
class MaxBinaryHeap(object):
def __init__(self):
self.heaplist = []
self.currentsize = 0
def max_percUp(self, i):
while ((i - 1) // 2) >= 0:
if self.heaplist[i] > self.heaplist[(i - 1) // 2]:
temp = self.heaplist[(i - 1) // 2]
self.heaplist[(i - 1) // 2] = self.heaplist[i]
self.heaplist[i] = temp
i = (i - 1) // 2
def max_insert(self, data):
self.heaplist.append(data)
self.currentsize += 1
self.max_percUp(self.currentsize - 1)
def max_delete(self, data):
index = self.heaplist.index(data)
if index == self.currentsize - 1:
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
else:
self.heaplist[index] = self.heaplist[-1]
self.heaplist = self.heaplist[:-1]
self.currentsize -= 1
self.max_percDown(index)
def maxChild(self, i):
if i * 2 + 2 > self.currentsize - 1:
return i * 2 + 1
else:
if self.heaplist[i * 2 + 1] > self.heaplist[i * 2 + 2]:
return i * 2 + 1
else:
return i * 2 + 2
def max_percDown(self, i):
while i * 2 + 1 <= self.currentsize - 1:
mc = self.maxChild(i)
if self.heaplist[i] < self.heaplist[mc]:
temp = self.heaplist[mc]
self.heaplist[mc] = self.heaplist[i]
self.heaplist[i] = temp
i = mc
def buildmaxHeap(self, data):
i = len(data) // 2 - 1
self.heaplist = data
self.currentsize = len(data)
while i >= 0:
self.max_percDown(i)
i = i - 1
参考文献
堆 (数据结构)-维基百科
二叉堆(一)之 图文解析 和 C语言的实现
二叉堆-维基百科
Python数据结构——二叉堆的实现
