数据结构——哈希表
2019-01-05
1 构造散列函数
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
- 直接定址法: 取关键字或关键字的某个线性函数值为散列地址。即
$hash(k)=k$或$hash(k)=a\cdot k+b$,其中$a,b$为常数(这种散列函数叫做自身函数); - 除留余数法: 取关键字被某个不大于散列表表长
$m$的数$p$除后所得的余数为散列地址。即$ hash(k)=k\,{\bmod \,}p,p\leq m$。不仅可以对关键字直接取模,也可在折叠法、平方取中法等运算之后取模。对$p$的选择很重要,一般取素数或$m$,若$p$选择不好,容易产生冲突。 - 数字分析法: 假设关键字是以
$r$为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。比如:比如有一组value1=112233,value2=112633,value3=119033,针对这样的数我们分析数中间两个数比较波动,其他数不变。那么我们取key的值就可以是key1=22,key2=26,key3=90。 - 折叠法: 将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。比如value=135790,要求key是2位数的散列值。那么我们将value变为13+57+90=160,然后去掉高位“1”,此时key=60,哈哈,这就是他们的哈希关系,这样做的目的就是key与每一位value都相关,来做到“散列地址”尽可能分散的目地。
- 随机数法
- 平方取中法
2 处理冲突
2.1 开放定址法
开放定址的意思是当发生冲突时,我们从当前位置向后按某种策略遍历哈希表。当发现可用的空间的时候,则插入元素。 开放地址有一次探测、二次探测和双重哈希。一次探测是指我们的遍历策略是一个线性函数,比如依次遍历冲突位置之后的第 1,2,3…N 位置。如果直接遍历 1,4(=2^2),9 (=3^2),这就是二次探测的一个例子。双重哈希就是遍历策略间隔由另一个哈希函数来确定。
下图是开放地址解决冲突问题的一个例子。key “John Smith” 和 “Sandra Dee” 在 index = 152 位置出现冲突,使用开放地址的方法将 “Sandra Dee” 存放在 index = 153 的位置。之后 key “Ted Baker” 的映射位置为 index = 153,又出现冲突,则将其存放在 index = 154 的位置。由这个例子我们可以看出这种处理方法的一个缺点:解决旧问题的同时会引入新的问题。
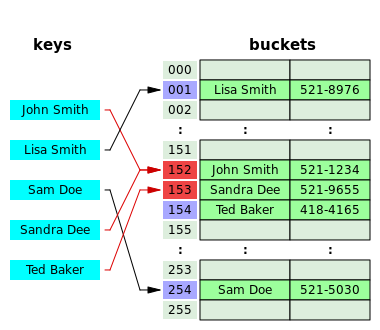
2.2 拉链法
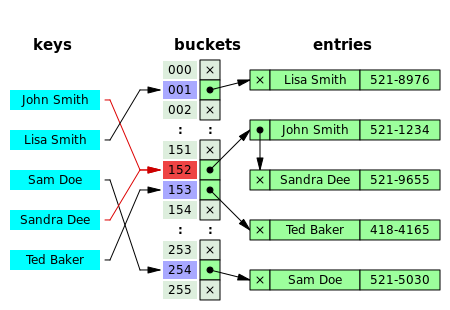
拉链法的思想是哈希表中的每个元素都是一个类似链表或者其他数据结构的 head。当出现冲突时,我们就在链表后面添加元素。 这也就意味着,如果某一个位置冲突过多的话,插入的时间复杂段将退化为 O(N)。补充一点,如果哈希表的每个元素都是一个链表头的,那么又可以分为头存储元素和不存储元素两种,如下图所示。

3 总结
简单比较一下这两种处理方法的优劣:开放定址在解决当前冲突的情况下同时可能会导致新的冲突,而开链不会有这种问题。同时开链相比于开放定址局部性较差,在程序运行过程中可能引起操作系统的缺页中断,从而导致系统颠簸。
