数据结构——二叉树

2019-01-05

数据结构与算法

1 树的基本术语

节点的度：节点拥有子树的数目
叶子：度为零的节点
分枝结点：度不为零的节点
树的度：树中节点的最大的度
层次：根节点的层次为1，其余节点的层次等于该节点的双亲节点的层次加1
树的高度：树中节点的最大层次

2 二叉树的性质

性质1：二叉树第 $i$ 层的节点数目最多为 $2^n (n=i-1,i>=1)$
性质2：深度为 $k$ 的二叉树至多有 $2^k-1(k>=1)$ 个节点
性质3：包含 $n$ 个节点的二叉树的高度至少为 $log_2(n+1)$
性质4：在任意一棵二叉树中，若叶子节点的个数为 $n_0$ ，度为2的节点的个数为 $n_2$ ，那么 $n_0=n_2+1$
性质5：如果T2是由有序树T转换而来的二叉树，那么T中结点的前序就是T2中结点的前序，T中结点的后序就是T2中结点的中序。

3 满二叉树

定义：高度为 $h$ ，并且节点数是 $2^h-1$ ，则称为满二叉树。

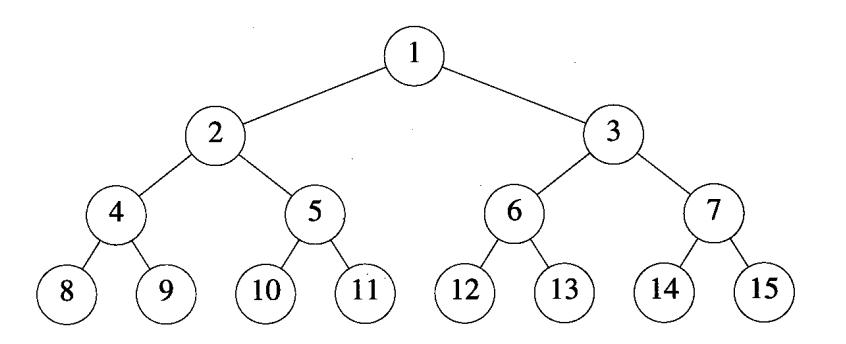
4 完全二叉树

定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

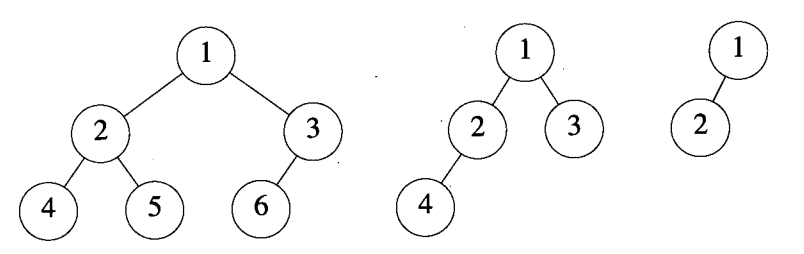
5 二叉查找树

定义：又称为二叉搜索树，设 $x$ 为二叉查找树的一个节点， $x$ 节点的值为 $x.val$ 。如果 $y$ 是 $x$ 的左子树中的一个节点，则 $y.val<=x.val$ ；如果 $y$ 是 $x$ 的右子树中的一个节点，则 $y.val>=x.val$ 。

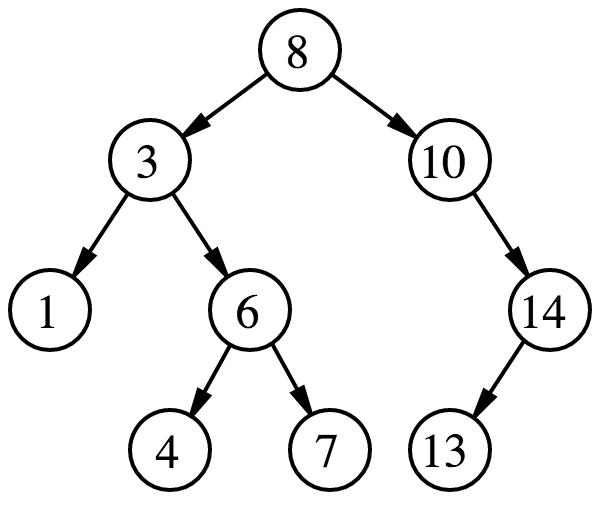
特点：

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

6 二叉树的实现（Python）

用Python实现二叉树可以通过两种方式，分别是使用List实现和使用类实现。

6.1 使用List实现

# 实现二叉树(用 list 实现)
# -*- coding: utf-8 -*-
# 初始化
def BinaryTree(data):
    return [data,[],[]]

def insertLeft(tree, data):
    leftSubTree = tree.pop(1)
    if leftSubTree: # 判断当前这个树的左子树是否为空
        tree.insert(1, [data, leftSubTree, []]) # 不为空，将数插入，并将原左子树作为该数的左子树
    else:
        tree.insert(1, [data, [], []])
    return tree

def insertRight(tree, data):
    rightSubTree = tree.pop(2)
    if rightSubTree:
        tree.insert(2, [data, [], rightSubTree])
    else:
        tree.insert(2, [data, [], []])
    return tree

def getLeftChild(tree):
    return tree[1]

def getRightChild(tree):
    return tree[2]

if __name__ == '__main__':
    tree = BinaryTree('a')
    print(tree)
    insertLeft(tree, 'b')
    print(tree)
    insertRight(tree, 'c')
    print(tree)
    insertLeft(tree, 'd')
    print(tree)
    insertLeft(getLeftChild(getLeftChild(tree)), 'f')
    print(tree)

# 输出
['a', [], []]
['a', ['b', [], []], []]
['a', ['b', [], []], ['c', [], []]]
['a', ['d', ['b', [], []], []], ['c', [], []]]
['a', ['d', ['b', ['f', [], []], []], []], ['c', [], []]]

使用类实现

## 6.2 实现二叉树(用类实现)
# -*- coding: utf-8 -*-
class BinaryTree(object):
    def __init__(self, data):
        self.__key = data
        self.__leftChild = None
        self.__rightChild = None

    def getKey(self):
        return self.__key

    def getLeft(self):
        return self.__leftChild

    def setLeft(self, tree):
        self.__leftChild = tree

    def getRight(self):
        return self.__rightChild

    def setRight(self, tree):
        self.__rightChild = tree

    def insertLeft(self, data):
        if self.__leftChild == None:
            # self.__leftChild = BinaryTree(data)
            self.setLeft(BinaryTree(data))
        else:
            t = BinaryTree(data)
            t.setLeft(self.getLeft())
            self.setLeft(t)
            # t.__leftChild = self.__leftChild
            # self.__leftChild = t

    def insertRight(self, data):
        if self.__rightChild == None:
            self.setRight(BinaryTree(data))
            # self.__rightChild = BinaryTree(data)
        else:
            t = BinaryTree(data)
            self.setRight(self.getRight())
            self.setRight(t)
            # t.__rightChild = self.__rightChild
            # self.__rightChild = t

    # 树的先序遍历
    def preorder(self, nodelist = None):
        if nodelist is None:
            nodelist = []
        if self:
            nodelist.append(self.getKey())
            if self.getLeft():
                self.getLeft().preorder(nodelist)
            if self.getRight():
                self.getRight().preorder(nodelist)
        return nodelist

    # 中序遍历，使用递归，返回list
    def inorder(self, nodelist = None):
        if nodelist is None:
            nodelist = []
        if self:
            if self.getLeft():
                self.getLeft().inorder(nodelist)
            nodelist.append(self.getKey())
            if self.getRight():
                self.getRight().inorder(nodelist)
        return nodelist

    # 中序遍历，使用递归，直接输出
    def inorder1(self):
        if self:
            if self.getLeft():
                self.getLeft().inorder1()
            print(self.getKey())
            if self.getRight():
                self.getRight().inorder1()

    # 后序遍历
    def postorder(self, nodelist = None):
        if nodelist is None:
            nodelist = []
        if self:
            if self.getLeft():
                self.getLeft().postorder(nodelist)
            if self.getRight():
                self.getRight().postorder(nodelist)
            nodelist.append(self.getKey())
        return nodelist

if __name__ == '__main__':
    tree = BinaryTree('a')
    tree.insertLeft('b')
    tree.insertRight('c')
    tree.getLeft().insertRight('d')
    node = tree.preorder()
    print(node)
    node1 = tree.inorder1()
    print(node1)
    node2 = tree.postorder()
    print(node2) 
    
# 输出
['a', 'b', 'd', 'c']
b
d
a
c
None
['d', 'b', 'c', 'a']

 数据结构——二叉查找树数据结构——哈希表 