数据结构——二叉查找树

2019-01-05

数据结构与算法

1 基础概念

定义：又称为二叉搜索树，设 $x$ 为二叉查找树的一个节点， $x$ 节点的值为 $x.val$ 。如果 $y$ 是 $x$ 的左子树中的一个节点，则 $y.val<=x.val$ ；如果 $y$ 是 $x$ 的右子树中的一个节点，则 $y.val>=x.val$ 。

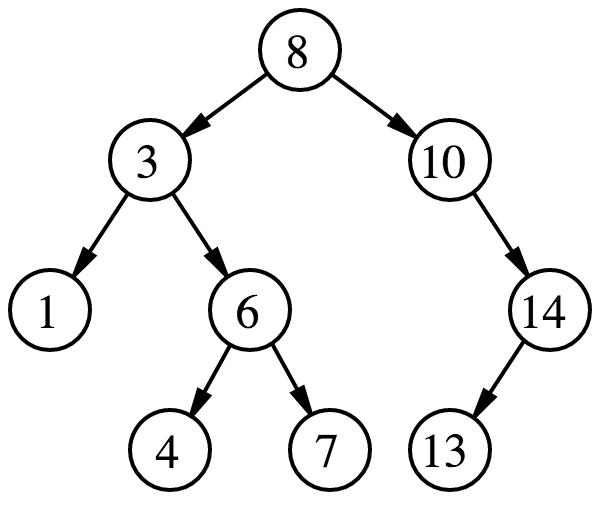
特点：

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

2 代码实现

2.1 节点定义

class BinarySearchTree(object):
    def __init__(self, key):
        self.__key = key
        self.__leftChild = None
        self.__rightChild = None
        self.__parent = None  # 父节点

2.2 查找

2.2.1 递归版本

# 查找 key值
def find(self, data):
    if data == self.getKey():
        return self
    elif data < self.getKey() and self.getLeftChild():
        return self.getLeftChild().find(data)
    elif data > self.getKey() and self.getRightChild():
        return self.getRightChild().find(data)
    else:
        return None

2.2.2 非递归版本

def find1(self, data):
    while data != self.getKey():
        if data < self.getKey():
            self = self.getLeftChild()
        else:
            self = self.getRightChild()
    return self

2.3 获取最大最小结点

# 返回树中的最小元素与最大元素的结点
def findMin(self):
    if self.getLeftChild():
        return self.getLeftChild().findMin()
    else:
        return self

def findMax(self):
    tree = self
    if tree:
        while tree.getRightChild():
            tree = tree.getRightChild()
    return tree

2.4 前驱和后继

节点的前驱：是该节点的左子树中的最大节点。
节点的后继：是该节点的右子树中的最小节点。

# 前驱和后继节点
def predecessor(self):
    curNode = self
    # 如果 curNode存在左孩子，则 "curNode的前驱结点"为"以其左孩子为根的子树的最大结点"
    if curNode.getLeftChild():
        return curNode.getLeftChild().findMax()
    # 如果 curNode没有左孩子。则 curNode有以下两种可能：
    # (1) curNode是"一个右孩子"，则 "curNode的前驱结点"为 "它的父结点"
    # (2) curNode是"一个左孩子"，则查找 "curNode的最低的父结点，并且该父结点要具有右孩子"，
    #     找到的这个"最低的父结点"就是 "curNode的前驱结点"
    preNode = curNode.getParent()
    while preNode and curNode == preNode.getLeftChild():
        curNode = preNode
        preNode = preNode.getParent()
    return preNode

def successor(self):
    curNode = self
    # 如果 curNode存在右孩子，则 "curNode的后继结点"为"以其右孩子为根的子树的最小结点"
    if curNode.getRightChild():
        return curNode.getRightChild().findMin()
    # 如果 curNode没有右孩子。则 curNode有以下两种可能：
    # (1) curNode是"一个左孩子"，则 "curNode的后继结点"为"它的父结点"
    # (2) curNode是"一个右孩子"，则查找 "curNode的最低的父结点，并且该父结点要具有左孩子"，
    #     找到的这个"最低的父结点"就是 "curNode的后继结点"
    sucNode = curNode.getParent()
    while sucNode and curNode == sucNode.getRightChild():
        curNode = sucNode
        sucNode = sucNode.getParent()
    return sucNode

2.5 插入

# 为了将 data插入到树 Tree中，先用find查找，如果找到 data，则什么也不做。
# 否则，将 data插入到遍历路径的最后一点。
def insert(self, data):
    if data < self.getKey():
        if self.getLeftChild():
            self.getLeftChild().insert(data)
        else:
            tree = BinarySearchTree(data)
            tree.setParent(self)
            self.setLeftChild(tree)
    elif data > self.getKey():
        if self.getRightChild():
            self.getRightChild().insert(data)
        else:
            tree = BinarySearchTree(data)
            tree.setParent(self)
            self.setRightChild(tree)

2.6 删除

删除某节点有3种情况：

如果节点是一片树叶，那么可以立即被删除。
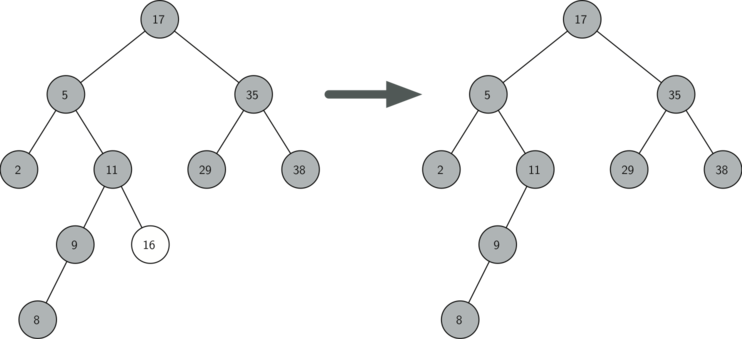
如果节点只有一个儿子，则将此节点parent的指针指向此节点的儿子，然后删除。
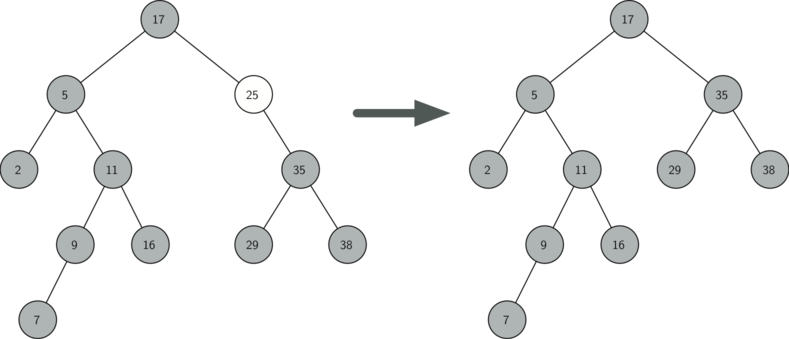
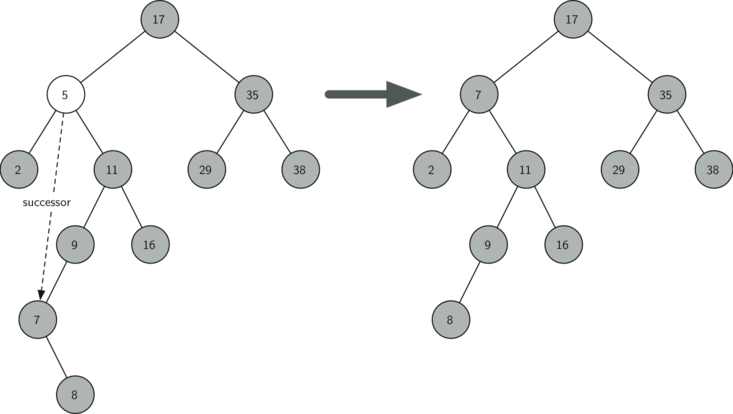
如果节点有两个儿子，则将其右子树的最小数据代替此节点的数据，并将其右子树的最小数据（不可能有左儿子，只有一个右儿子）删除。

def delete(self, data):
    if self is None:
        return self
    if data < self.getKey():
        self.setLeftChild(self.getLeftChild().delete(data))
    elif data > self.getKey():
        self.setRightChild(self.getRightChild().delete(data))
    elif self.getLeftChild() and self.getRightChild():
        data_min = self.getRightChild().findMin().getKey()
        self.setKey(data_min)
        self.setRightChild(self.getRightChild().delete(data_min))
    elif self.getLeftChild():
        self = self.getLeftChild()
    elif self.getRightChild():
        self = self.getRightChild()
    else:
        self = None
    return self

2.7 完整实现

# 实现二叉查找树
# -*- coding: utf-8 -*-

class BinarySearchTree(object):
    def __init__(self, key):
        self.__key = key
        self.__leftChild = None
        self.__rightChild = None
        self.__parent = None

    def getKey(self):
        return self.__key

    def setKey(self, data):
        self.__key = data

    def setLeftChild(self, tree):
        self.__leftChild = tree

    def getLeftChild(self):
        return self.__leftChild

    def setRightChild(self, tree):
        self.__rightChild = tree

    def getRightChild(self):
        return self.__rightChild

    def setParent(self, tree):
        self.__parent = tree

    def getParent(self):
        return self.__parent

    # 查找key值
    def find(self, data):
        if data == self.getKey():
            return self
        elif data < self.getKey() and self.getLeftChild():
            return self.getLeftChild().find(data)
        elif data > self.getKey() and self.getRightChild():
            return self.getRightChild().find(data)
        else:
            return None

    def find1(self, data):
        while data != self.getKey():
            if data < self.getKey():
                self = self.getLeftChild()
            else:
                self = self.getRightChild()
        return self

    # 返回树中的最小元素与最大元素的结点
    def findMin(self):
        if self.getLeftChild():
            return self.getLeftChild().findMin()
        else:
            return self

    def findMax(self):
        tree = self
        if tree:
            while tree.getRightChild():
                tree = tree.getRightChild()
        return tree

    # 前驱和后继节点
    def predecessor(self):
        curNode = self
        # 如果curNode存在左孩子，则"curNode的前驱结点"为"以其左孩子为根的子树的最大结点"
        if curNode.getLeftChild():
            return curNode.getLeftChild().findMax()
        # 如果curNode没有左孩子。则curNode有以下两种可能：
        # (1) curNode是"一个右孩子"，则"curNode的前驱结点"为 "它的父结点"
        # (2) curNode是"一个左孩子"，则查找"curNode的最低的父结点，并且该父结点要具有右孩子"，
        #     找到的这个"最低的父结点"就是"curNode的前驱结点"
        preNode = curNode.getParent()
        while preNode and curNode == preNode.getLeftChild():
            curNode = preNode
            preNode = preNode.getParent()
        return preNode

    def successor(self):
        curNode = self
        # 如果curNode存在右孩子，则"curNode的后继结点"为"以其右孩子为根的子树的最小结点"
        if curNode.getRightChild():
            return curNode.getRightChild().findMin()
        # 如果curNode没有右孩子。则curNode有以下两种可能：
        # (1) curNode是"一个左孩子"，则"curNode的后继结点"为"它的父结点"
        # (2) curNode是"一个右孩子"，则查找"curNode的最低的父结点，并且该父结点要具有左孩子"，
        #     找到的这个"最低的父结点"就是"curNode的后继结点"
        sucNode = curNode.getParent()
        while sucNode and curNode == sucNode.getRightChild():
            curNode = sucNode
            sucNode = sucNode.getParent()
        return sucNode

    # 为了将data插入到树Tree中，先用find查找，如果找到data，则什么也不做。否则，将data插入到遍历路径的最后一点。
    def insert(self, data):
        if data < self.getKey():
            if self.getLeftChild():
                self.getLeftChild().insert(data)
            else:
                tree = BinarySearchTree(data)
                tree.setParent(self)
                self.setLeftChild(tree)
        elif data > self.getKey():
            if self.getRightChild():
                self.getRightChild().insert(data)
            else:
                tree = BinarySearchTree(data)
                tree.setParent(self)
                self.setRightChild(tree)

    # 删除某节点有3种情况：
    # 1.如果节点是一片树叶，那么可以立即被删除。
    # 2.如果节点只有一个儿子，则将此节点parent的指针指向此节点的儿子，然后删除。
    # 3.如果节点有两个儿子，则将其右子树的最小数据代替此节点的数据，并将其右子树
    # 的最小数据（不可能有左儿子，只有一个右儿子）删除。
    def delete(self, data):
        if self is None:
            return self
        if data < self.getKey():
            self.setLeftChild(self.getLeftChild().delete(data))
        elif data > self.getKey():
            self.setRightChild(self.getRightChild().delete(data))
        elif self.getLeftChild() and self.getRightChild():
            data_min = self.getRightChild().findMin().getKey()
            self.setKey(data_min)
            self.setRightChild(self.getRightChild().delete(data_min))
        elif self.getLeftChild():
            self = self.getLeftChild()
        elif self.getRightChild():
            self = self.getRightChild()
        else:
            self = None
        return self

    # 树的先序遍历
    def preorder(self, nodelist = None):
        if nodelist is None:
            nodelist = []
        if self:
            nodelist.append(self.getKey())
            if self.getLeftChild():
                self.getLeftChild().preorder(nodelist)
            if self.getRightChild():
                self.getRightChild().preorder(nodelist)
        return nodelist

if __name__ == '__main__':
    tree = BinarySearchTree(17)
    tree.insert(5)
    tree.insert(35)
    tree.insert(2)
    tree.insert(29)
    tree.insert(11)
    node = tree.preorder()
    print('先序遍历：',node)
    print('树的最小结点值：',tree.findMin().getKey())
    print('树的最大结点值：',tree.findMax().getKey())
    print('查找节点操作')
    print(tree.find(2).getKey())
    print(tree.find1(2).getKey())
    print('查找节点前驱和后继结点操作')
    print(tree.find(5).predecessor().getKey())
    print(tree.find1(11).successor().getKey())
    print('删除节点操作')
    t = tree.delete(5)
    print('先序遍历：',node)
    
输出：
先序遍历： [17, 5, 2, 11, 35, 29]
树的最小结点值： 2
树的最大结点值： 35
查找节点操作
2
2
查找节点前驱和后继结点操作
2
17
删除节点操作
先序遍历： [17, 5, 2, 11, 35, 29]

 数据结构——B树及其变体结构数据结构——二叉树 